1. ABCD - квадрат со стороной 20, а площадь поверхности призмы равна 1760. Sп=2So+Sб или 1760=2*20*20+Sб. => Sбок=1760-800=960. Sбок=4*Sграни => Sграни= 960:4=240. Sграни=сторона основания, умноженная на боковое ребро. Боковое ребро равно 240:20=12.
ответ: 12 ед.
2. ABCD - квадрат. АС=24, АС=BD (диагонали квадрата), DO=12 (как половина диагонали), SD=15. По Пифагору SO=√(SD²-DO²)=√(225-144) =√81 = 9 ед.
ответ: SO=9 ед.
3. Sсеч = 2*R*h = 4 (прямоугольник). Sбок= 2*π*R*h = 4π (боковая поверхность).
ответ: Sбок/π = 4 ед.
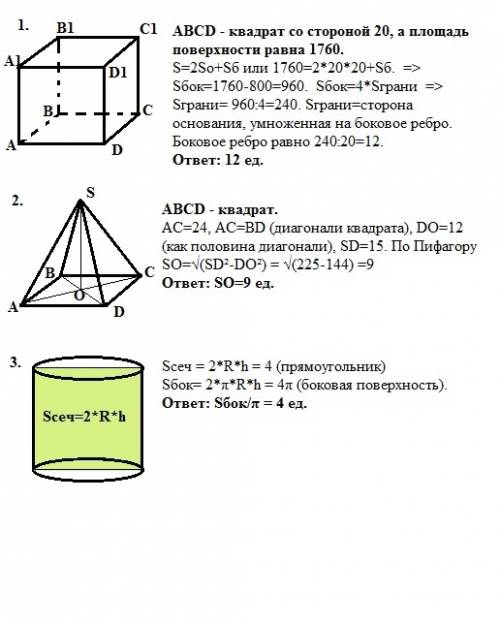
1. ABCD - квадрат со стороной 20, а площадь поверхности призмы равна 1760. Sп=2So+Sб или 1760=2*20*20+Sб. => Sбок=1760-800=960. Sбок=4*Sграни => Sграни= 960:4=240. Sграни=сторона основания, умноженная на боковое ребро. Боковое ребро равно 240:20=12.
ответ: 12 ед.
2. ABCD - квадрат. АС=24, АС=BD (диагонали квадрата), DO=12 (как половина диагонали), SD=15. По Пифагору SO=√(SD²-DO²)=√(225-144) =√81 = 9 ед.
ответ: SO=9 ед.
3. Sсеч = 2*R*h = 4 (прямоугольник). Sбок= 2*π*R*h = 4π (боковая поверхность).
ответ: Sбок/π = 4 ед.

Дано:
△DBC - прямоугольный.
∠C = 90˚
CK - высота.
DB = 20 см.
BC = 10 см.
Решение.
ЕСЛИ КАТЕТ РАВЕН ПОЛОВИНЕ ГИПОТЕНУЗЫ, ТО НАПРОТИВ ЛЕЖАЩИЙ УГОЛ РАВЕН 30°
=> ∠D = 30˚
СУММА ОСТРЫХ УГЛОВ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВНЯЕТСЯ 90°
=> ∠B = 90 - 30 = 60˚
△DCK и △BCK - прямоугольные т.к. CK - высота.
=> ∠KCB = 90 - 60 = 30˚
ЕСЛИ УГОЛ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВЕН 30°, ТО НАПРОТИВ ЛЕЖАЩИЙ КАТЕТ РАВЕН ПОЛОВИНЕ ГИПОТЕНУЗЫ.
=> BK = 10 : 2 = 5 см.
ответ: 5 см.