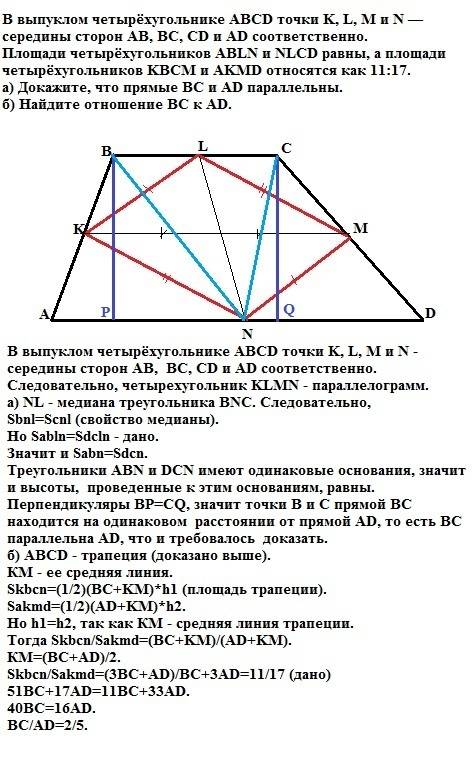
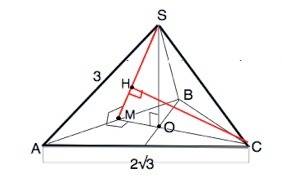
Расстояние от точки до плоскости равно длине отрезка, проведенного перпендикулярно к этой плоскости.
Проведем через ребро SC и высоту пирамиды плоскость перпендикулярно плоскости ASB.
SM⊥АВ и СМ⊥АВ. Отрезок СН лежит в плоскости MSC, он перпендикулярен линии пересечения плоскостей SM ⇒
CH перпендикулярен плоскости ASB
Искомое расстояние равно длине СН.
Основание правильной треугольной пирамиды - правильный треугольник. Все его стороны равны, все углы равны 60°⇒
1) СМ=АС•sin60°=2√3•√3:2=3
2) SM=√(SA²-AM²)
AM=AB:2=√3
SM=√(9-3) =√6
3) SO=√(SM²-OM²)
OM=CM:3 =1( медианы точкой пересечения делятся в отношении 2:1)
SO=√(6-1)=√5
4) sin ∠SMC=SO:SM=√5:√6
5) CH=CM•sin SMC=3•√5:√6=(√5•√2•√3):2=√15:√2 или √(15/2)
Обозначим половину второй диагонали за d.
По теореме Пифагора:
d = √(√34)² - (1/2•6)² = √34 - 3² = √34 - 9 = √25 = 5 см.
Тогда ася диагональ равна 5•2 см = 10 см.
ответ: 10 см.