<BlaC=58°, <AlcB=48°.
Объяснение:
В треугольнике АВС внешний угол С (BCD) равен сумме двух внутренних, не смежных с ним, то есть
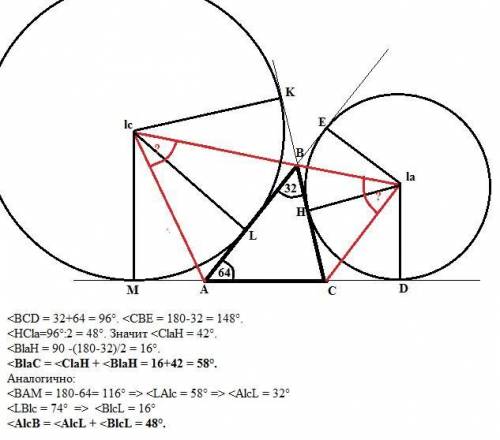
<BCD = 32+64 = 96°. Внутренний угол С равен 84°, как смежный с ним.
Внешний угол СВЕ равен 148° (аналогично).
Точки D, H и Е - точки касания окружности с центром la с прямыми, содержащими стороны треугольника АВС. Точки K, L и М - точки касания окружности с центром lc с прямыми, содержащими стороны треугольника АВС.
СН и СD - касательные из точки С к окружности с центром la. Следовательно, прямая Сla - биссектриса угла BCD по свойству касательных к окружности из одной точки. Итак, в прямоугольном треугольнике СНla (точка Н - точка касания, в которой радиус перпендикулярен касательной) угол HCla=96°:2 = 48°. Значит <ClaH = 42° (по сумме острых углов прямоугольного треугольника).
Точно так же в прямоугольном треугольнике НВla угол
<BlaH = 90 -(180-32)/2 = 16°.
Значит <BlaC = <ClaH + <BlaH = 16+42 = 58°.
Аналогичные рассуждения и относительно вневписанной окружности с центром в точке lc.
<BAM = 180-64= 116° => <LAlc = 58° => <AlcL = 32°
<LBlc = 74° => <BlcL = 16°
<AlcB = <AlcL + <BlcL = 48°.
Можно проще: Так как Аlc и Blc - биссектрисы, <BAlc = <BAM:2 = 58°, a
<ABlc = <KBL:2 = (180-32)/2 = 74° Тогда в треугольнике AlcB по сумме внутренних углов треугольника
<AlcB = 180 - 58 - 74 = 48°.
Точно так же: Сla и Bla - биссектрисы,
<BCla = <BCD:2 = 96:2 =48°, a
<CBla = <EBH:2 = (180-32)/2 = 74° Тогда в треугольнике ВlаС по сумме внутренних углов треугольника
<ВlаС = 180 - 48 - 74 = 58°.
Проведем прямую СР параллельно диагонали BD до пересечения с продолжением основания AD в точке Р. BCPD параллелограмм и DP=BC.
Треугольник АСР прямоугольный и равнобедренный, так как катеты CP и АС перпендикулярны (АС перпендикулярна BD - дано, а CP параллельна BD по построению).
Пусть катеты AC и CР равны X. Тогда гипотенуза AP=Х√2 (по Пифагору).
CH - высота треугольника АСР, проведенная из вершины прямого угла и равна произведению катетов, деленному на гипотенузу (свойство).
Итак, CH=AC*CP/AP. CH=14см (дано). Тогда
14=Х^2/(Х√2). Отсюда Х=14√2, а АР=14√2*√2=28см.
Но АР=AD+BC. Тогда площадь трапеции равныS=(AD+BC)*CH/2 или S=28*14/2=196 см^2.
ответ: S=196 см^2.