АВСД - равнобедреная трапеция
АД = 24 , ВС = 6
АВ = СД , углы А и Д равны
ВК = СЛ высоты трапеции
равнобедреные треуольники АВК и ДСЛ равны
АВ + ВС + СД + АД - периметр трапеции
АД + ВС = АВ + СД ( в любом описанном четырёхугольнике суммы противоположных сторон равны )
АВ + СД = 24 +6 = 30
АВ = СД = 30 : 2 = 15
АК = ДЛ
КЛ = ВС = 6 ( ВСЛК - прямоугольник)
АК = ДЛ = ( 24 - 6 ) : 2 = 9
ВК в квадрате = 15 в квадрате - 9 в квадрате = 144
ВК = 12
А так как диаметр окружности является высотой пирамиды то радиус = 12 : 2 = 6
ΔABC - равнобедренный, AB = BC;
AC = 24 см; BM⊥AC; BM = 9 см
Площадь треугольника
S = AC * BM / 2 = 24 * 9 /2 = 108 см²
BM - высота равнобедренного треугольника, она же и медиана.
⇒ AM = MC = 24/2 = 12 см
ΔBMC - прямоугольный, ∠M = 90°.
Теорема Пифагора
BC² = BM² + MC² = 9² + 12² = 81 + 144 = 225 = 15² ⇒
AB = BC = 15 см
Площадь треугольника можно посчитать через радиус вписанной окружности:
S = pr, где p - полупериметр. ⇒ r = S/p
см
r = S/p = 108 / 27 = 4 см
ответ: радиус вписанной окружности 4 см
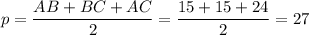
H =6 см; R =4 см . Осевое сечение прямоугольник одна сторона которой диаметр основания, другая высота цилиндра . Площадь осевого сечения : S =2R'H =2'4 см'6 см =48 см2