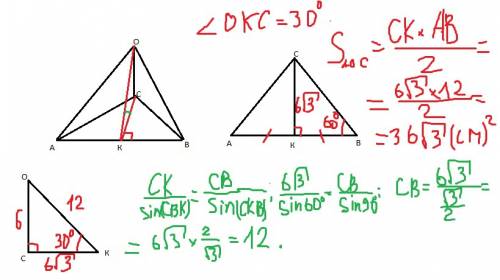
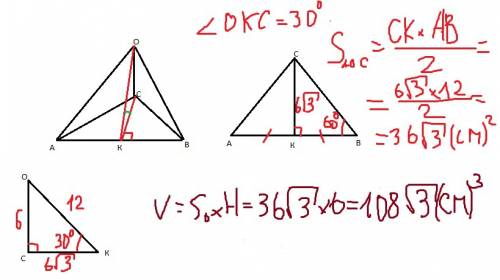
1) квадрат и треугольник взаимно перпендикулярны, значит, ВС перпендикулярна плоскости треугольника АМВ, следовательно ВС перпендикулярна любой прямой лежащей в плоскости АМВ, а значит, перпендикулярна и АМ.
2)проведём высоту МК в треугольнике АМВ. Так как треугольник равнобедренный, то высота является и медианой, поэтому АК=КВ=4:2=2
из прямоугольного треугольника МКВ МК^2=MB^2-BK^2=(2 корень из6)^2-4=4*6-4=20
из прямоугольного треугольника КВС КС^2=KB^2+BC^2=2^2+4^2=4+16=20
треугольник МКС равнобедренный значит угол КМС=углу МСК, угол МКС=90градусов так как МК перпендикулярна к плоскости квадрата, поэтому угол между МС и плоскостью квадрата равен 90градусов :2=45 градусов
Если площади тр-ков АВМ и СВМ относятся как 1:3, то и основания этих тр-ков АМ и СМ относятся как 1:3, потому что высоты у этих тр-ков одинаковы, а площадь тр-ка рана половине произведения основания на высоту. Обозначим х = АМ, тогда СМ = 3х.
Обозначим углы: уг.АВМ = уг.СВМ = алфа, уг. АМВ = бета, уг.СМВ = 180 - бета.
Рассмотрим тр-к АВМ: по теореме синусов sin алфа / х = sin бета / 4, откуда
sin алфа / sin бета = х/4 (1)
Рассмотрим тр-к СВМ: по теореме синусов sin алфа /3х = sin (180-бета) / ВС. Поскольку sin (180-бета) = sin бета , то
sin алфа / sin бета = 3х/ВС (2)
Приравняем правые части равенств (1) и (2)
х/4 = 3х/ВС, откуда ВС = 12
Используем неравенство треугольника для тр-ка АВС: сумма двех сторон всегда больше третьей стороны:
АВ + ВС > АС или 4+12 > 4х, получаем х < 4 (3)
АВ + АС > BC или 4 + 4х > 12 , получаем х > 2 (4)
Итак, 2<x<4. Принимаем х = 3, тогда 3х = 9 и АС = 4х =12
ответ: ВС= АС = 12