Геометрия - важный раздел математики. Ее возникновение уходит в глубь тысячелетий и связано прежде всего с развитием ремесел, культуры, искусств, с трудовой деятельностью человека и наблюдением окружающего мира. Об этом свидетельствуют названия геометрических фигур.
Например, название фигуры "трапеция" происходит от греческого слова "трапезион" (столик) , от которого произошли также слово "трапеза" и другие родственные слова. От греческого слова "конос" (сосновая шишка) произошло название "конус", а термин "линия" возник от латинского "линум" (льняная нить) .
Геометрические знания широко применяются в жизни - в быту, на производстве, в науке. При покупке обоев надо знать площадь стен комнаты; при определении расстояния до предмета, наблюдаемого с двух точек зрения, нужно пользоваться известными вам теоремами; при изготовлении технических чертежей - выполнять геометрические построения. И если ты, юный читатель, хорошо изучил курс геометрии, то не останешься безоружным, когда при решении практических задач потребуется применить геометрические теоремы или формулы.
Геометрия — важный раздел математики. Ее возникновение уходит в глубь тысячелетий и связано прежде всего с развитием ремесел, культуры, искусств, с трудовой деятельностью человека и наблюдением окружающего мира. Об этом свидетельствуют названия геометрических фигур.
Например, название фигуры «трапеция» происходит от греческого слова «трапезион» (столик) , от которого произошли также слово «трапеза» и другие родственные слова. От греческого слова «конос» (сосновая шишка) произошло название «конус» , а термин «линия» возник от латинского «линум» (льняная нить) .
Геометрические знания широко применяются в жизни — в быту, на производстве, в науке. При покупке обоев надо знать площадь стен комнаты; при определении расстояния до предмета, наблюдаемого с двух точек зрения, нужно пользоваться известными вам теоремами; при изготовлении технических чертежей — выполнять геометрические построения. И если ты, юный читатель, хорошо изучил курс геометрии, то не останешься безоружным, когда при решении практических задач потребуется применить геометрические теоремы или формулы.
только рисунок не банить...модераторы...(
апофема-высота боковой грани правильной пирамиды SF=f=√(h²+r²)(по т пифагора)
сюда только радиус подставить и высоту
√(8√2+8√2)=√(128+128)=√256=16
2)угол между боковой гранью и основанием
в лс разберем..
3) площадь поверхности пирамиды
Sпов=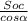
4)расстояние от центра основания пирамиды до плоскости боковой грани
___________
пусть ABCD основание, S -- вершина пирамиды, O -- центр основания, E -- середина AB
SO=8√2, SE=8√2
1)√(8√2+8√2)=√(128+128)=√256=16
2) SE и EO перпендикулярны AB, поэтому SEO -- искомый угол
tg SEO = SE/OE= 1, следовательно, SEO=45°
3) Площадь поверхности равна S=Sосн+Sбок
Sосн=AD^2
Sбок=4*(AB*SE)/2=2*AD*SE
4)разберем
5)в лс