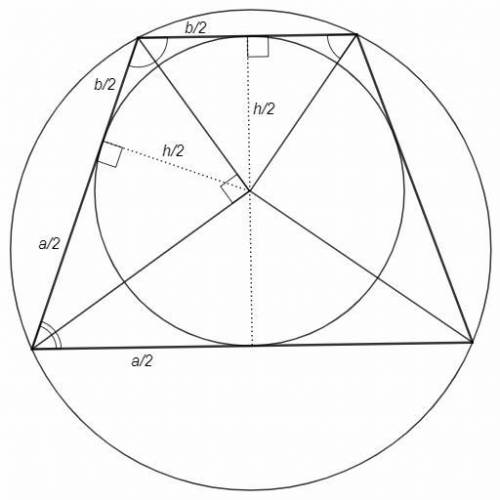
Трапеция описанная, следовательно её биссектрисы пересекаются в одной точке (центр вписанной окружности). Трапеция вписанная, следовательно равнобедренная, углы при основании равны. Значит равны их половины, биссектрисы углов при основании образуют равнобедренный треугольник. Перпендикуляр из центра вписанной окружности к основанию (радиус) является медианой.
Биссектрисы внутренних углов при параллельных пересекаются под прямым углом. Радиус в точку касания на боковой стороне - высота из прямого угла, она равна среднему пропорциональному проекций катетов. Отрезки касательных из одной точки равны, проекции катетов равны половинам оснований. Радиус равен половине высоты. Таким образом h=√(ab)
Угол СВD равен углу ADB - внутренние накрест лежащие углы при параллельных прямых BC и AD и секущей AD.
Угол ВСА равен углу САD -внутренние накрест лежащие углы при параллельных прямых BC и AD и секущей АС.
Из подобия треугольников АО:ОС=OD:OB=3:2
Треугольники ВОF и DEO подобны по двум углам:
Угол СВD равен углу ADB - внутренние накрест лежащие углы при параллельных прямых BC и AD и секущей AD.
Угол BOF равен углу DOE как вертикальные.
Из подобия треугольников:
BF: ED=BO:OD=2:3,
BF=2ED/3=2·15/3=10 см
ответ. 10 см.