Отметь, какие отрезки являются хордами окружности.
HF
OF, OH, OG
HE, HG, OE, OF
HE, HF, GF
Во
Дана окружность с центром O и её диаметры AB и CD.
Определи периметр треугольника AOD, если CB=13 см, AB=49 см.
ответ
51
Во
Даны основные конструкции, которые рассмотрены в теоретическом материале:
1. На данном луче от его начала отложить отрезок равный данному.
2. Построение угла равного данному.
3. Построение биссектрисы угла.
4. Построение перпендикулярных прямых.
5. Построение середины отрезка.
Составь план построения угла величиной 45 градусов (даны лист бумаги, карандаш, циркуль и линейка).
В ответах указаны номера шагов по порядку, шаги могут повторяться.
3,3
1,2,4
4,2,3
4,3
Во
Начерти окружности с данными центрами O и B и данными радиусами r1=15,5 см, r2=4,3 см так, чтобы они имели одну общую точку. Определи расстояние OB.
4,3
8,6
19,8 или 11,2
19
Во
На сколько частей делят окружность 3 диаметра?
ответ
Во
Определите количество разных треугольников, которые можно построить по трем сторонам а = 4, b = 3, c = 8.
ответ
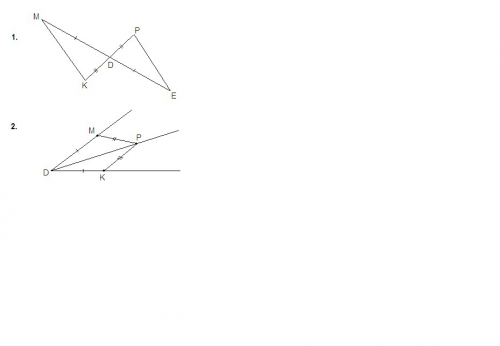
PD = DK по условию,
∠MDK = ∠EDP как вертикальные, ⇒
ΔMDK = ΔEDP по двум сторонам и углу между ними.
В равных треугольниках напротив равных сторон лежат равные углы, значит
∠KMD = ∠PED.
2. DM = DK по условию,
РМ = РК по условию,
DP - общая сторона для треугольников DMP и DKP, ⇒
ΔDMP = ΔDKP по трем сторонам.
В равных треугольниках напротив равных сторон лежат равные углы, значит ∠MDP = ∠KDP, следовательно
DP - биссектриса угла D.
3. Начертим окружность с центром в точке А произвольного радиуса (большего, чем расстояние до прямой ВС). Точки пересечения этой окружности с прямой ВС - К и М.
Начертим две окружности одинакового произвольного радиуса (большего половины отрезка КМ) с центрами в точках К и М.
Через точки пересечения этих окружностей (Е и F) проводим прямую.
EF ∩ BC = H. АН - искомая высота.
Прямая EF всегда пройдет через точку А, так как является серединным перпендикуляром к отрезку КМ, а точка А равноудалена от концов этого отрезка, а значит лежит на серединном перпендикуляре.