ДАНЫ ТОЧКИ А(9;-5;8), B(3;-6;4), C(-6;0;8).
1) Координаты вектора BC: (-6-3=-9; 0-(-6)=6; 8-4=4) = (-9; 6; 4).
2) Разложение вектора BC как суммы двух векторов.
ВС = ВА + АС.
Вектор ВА =(9-3=6; -5+6=1; 8-4=4) = (6; 1; 4),
Вектор АС = (-6-9=-15; 0+5=5; 8-8=0) = (-15; 5; 0).
ВС = (6-15 = -9; 1+5=6; 4+0=4) = (-9; 6; 4).
3) Координаты середины отрезка AB.
М = ((9+3)/2=6; (-5-6)/2=-5,5; (8+4)/2=6) = (6; -5,5; 6).
4) Длина отрезка AC.
|AC| = √((-15)² + 5² + 0²) = √(225 + 25 + 0) =√250 = 5√10.
5) Определите вид треугольника ABC.
Для этого надо определить или стороны, или углы треугольника.
Треугольник АВС
a(ВС) b(АС) c(АВ) p 2p S
11,53256 15,81139 7,28011 17,31203 34,62406 38,81043
133 250 53 (это квадраты сторон).
cos A = 0,73843 cos B = -0,381141 cos С = 0,90487
Аrad = 0,74005 Brad = 1,961827 Сrad = 0,439712
Аgr = 42,401914 Bgr = 112,404407 Сgr = 25,193679
Треугольник АВС тупоугольный.
6) Длина медианы из вершины А:
Точка М как середина стороны BC
х у z
-1,5 -3 6
А(9;-5;8)
Тогда АМ = √((9+1,5)² + (-5+3)² + (8-6)²) = √118,25 ≈ 10,87428.
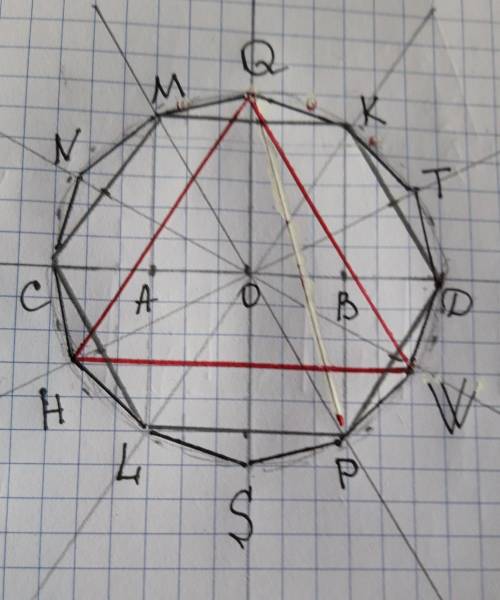
1) вписать правильный шестиугольник
Объяснение:
1)чертим горизонтальный диаметр,
2)делим диаметр на четыре равные части 3см÷4=1,5см
3)через середину каждого гортзонтального радиуса проводим вертикальные перпендикуляры(один перпендикуляр через т.А, другой через т.В.
4)т.С и т.Д - это точки пересечения горизонтального диаметра с окружностью
5)т.М, т.К. т.Р, т.L - это точки пересечения перпендикуляров с окружностью
6)соединяем последовательно точки С М К Д Р L построен правильный шестиугольник, вписанный в окпужность
Чтобы получить правильный вписанный 12 угольник, нужно провести дополнительно диаметры, проходящие через середины сторон СМ, МК, КД. На окружности получаем точки N, Q, T, W, S, H.Теперь последовательно соединяем вершины С, N, M, Q, K, T, D, W, P, S, L, H.Двенадцатиугольник СNMQKTDWPSLH является правильным 12 угольником, вписанным в окружность.
Чтобы получить правильный треуголдник, вписанный в окружность, надо соединить вершины НQW. Треугольник HQW является правильным треугольником, вписанным в окружпость.
Объяснение:
геометри на казазском