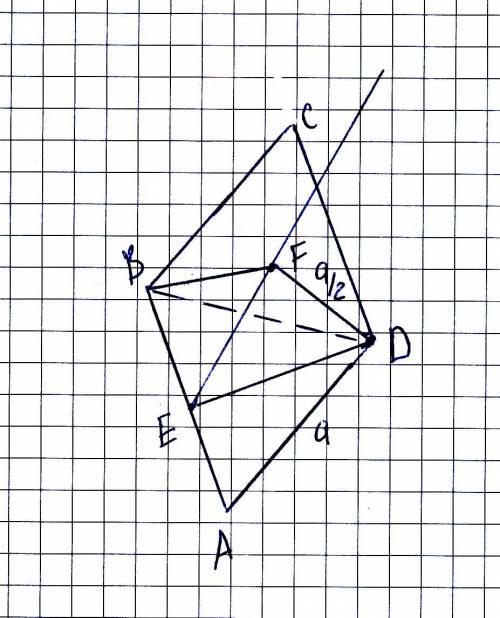
См чертеж.
ED перпендикулярно АВ, (ED = a*корень(3)/2; но для решения это не нужно:))
В ПЛОСКОСТИ, ПЕРПЕНДИКУЛЯРНОЙ АВ проводим ЕF так, чтобы DF = a/2;
Треугольник BDF - прямоугольный и DF перпендикулярна BF.
Действительно, DF перпендикулярна ЕF по построению, но DF лежит в плоскости, перпендикулярной АВ, то есть она перпендикулярна и АВ, а значит, и любой прямой в плоскости, проходящей через АВ и EF.
Поэтому BF - искомая проекция BD на BFE и её величину очень легко вычислить, если увидеть, что угол FBD равен 30 градусам (FD/BD = 1/2, малая диагональ равна стороне ромба).
ответ а*корень(3)/2;
Апофема грани, высота пирамиды и расстояние от основания высоты до основания апофемы образуют прямоугольный треугольник. из него найдем половину стороны основания.
1/2 стороны основания= √(4а² - (а√2)²)=4а²-2а²=√2а² и равна а√2
а сторона основания равна 2а√2
Поскольку высота и половина основания равны в этом прямоугольном треугольнике, он - равнобедренный и угол между апофемой и средней линией квадрата в основании, что равносильно углу между боковой гранью и основанием,
равен 45 градусам.
Расстояние от центра основания пирамиды - перпендикуляр к апофеме. Поскольку угол между апофемой и плоскостью основания 45 градусов, получится равнобедренный прямоугольный треугольник с гипотенузой= половине стороны основания и катетами, равными половине апофемы = а.
Расстояние от центра основания до плоскости боковой грани =а
Площадь поверхности пирамиды равна сумме площади основания и площади боковой поверхности.
S основания =(2а√2)²=8а²
S боковая =4* 2а*а√2 =8а²√2
S полная =8а²√2+8а²=8а²(√2+1)