a) 1) Найдем координаты точки О. Для этого надо решить систему y=x+4 и y=-2x+1. Вычтем из первого уравнения второе, получим: 0=3x+3, x=-1 Подставим в первое y=-1+4=3. Итак, координаты центра О(-1; 3). 2) Найдем длину радиуса, используя координаты точки В, по формуле R^2=(2+1)^2 + (-1-3)^2 =9+16=25; 3) Запишем уравнение окружности
(x+1)^2 +(y-3)^2=25
б) У точек пересечения окружности с осью ОХ ординаты равны 0, поэтому подставим у=0 в уравнение окружности: (х+1)^2+9=25, x+1=+-4. Координаты этих точек (-4; 0) и (4; 0)
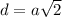, где d = AH - диагональ квадрата, a - сторона квадрата, которая нам известна (7м).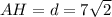
.
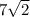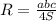, где a, b и c - стороны треугольника, а S - площадь треугольника.
;
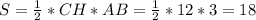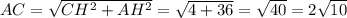
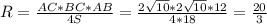
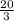м. 
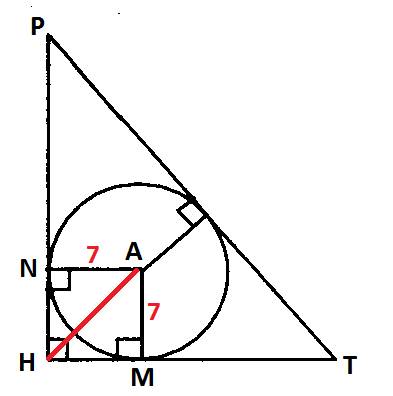
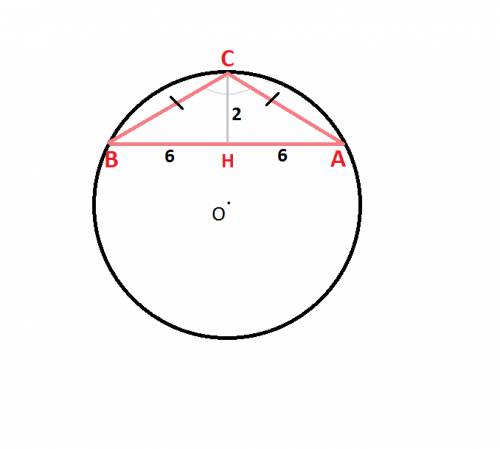
8 см
Решение на фотографии
Объяснение:
Свойство: катет прям. тр., лежащий против угла в 30гр., равен половине гипотенузы
гипотенуза в 2 раза больше этого катета