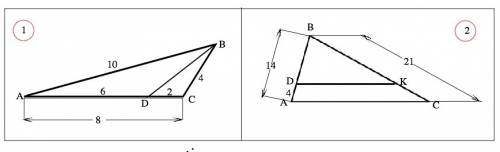
1) DC=AC-AD=8-6=2 см. Угол С общий для треугольников АВС и DВС, стороны, содержащие этот угол, пропорциональны (АС:ВС=ВС:DC=2). Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключенные между этими сторонами, равны, то такие треугольники подобны. Из подобия следует АВ:ВD=2, ⇒ BD=10:2=5 см
———————————
2) Обозначим К точку пересечения прямой из т.D с ВС. По условию DK||АС, тогда стороны АВ и ВС треугольника являются секущими для них. ⇒ соответственные углы при DK и АС равны, треугольники АВС и DBK подобны по равным углам. Из подобия следует АВ:DB=ВC:ВK. ВD=AB-AD=10. ⇒ 14:10=21:ВК ⇒ ВК=210:14=15 см. Поэтому КС=21-15=6 см. Сторона ВС делится на отрезки 15 см и 6 см.
8. <DBC=63°
9. P = 36 ед.
10. Не полное условие.
Объяснение:
Дуга BD равна 2*27° = 54° (так как вписанный угол, опирающийся на эту дугу, равен половине градусной меры этой дуги).
Дуга BDAC = 180°, так как ВС - диаметр.
Дуга DAC = DDAC - BD = 180-54 = 126°. =>
<DBC = 63° (вписанный, равен половине градусной меры дуги, на которую он опирается).
9. Биссектрисы углов параллелограмма отсекают от него равнобедренные треугольники. В нашем случае эти биссектрисы имеют общую точку Е на стороне ВС. Значит
АВ = ВЕ и EC = CD => BC = 2AB.
AB = СD и BC = AD (противоположные стороны параллелограмма).
Рabcd = 6*AB = 36 ед.