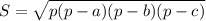, здесь a,b,c - стороны треугольника, p - полупериметр треугольника (в нашем случае a=4, b=13, c=15, 
).
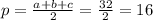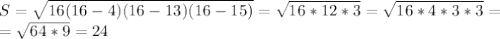
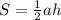, где a - сторона треугольника, h - проведённая к ней высота. Обозначим за h₁ высоту, проведённую к стороне a, за h₂ высоту, проведённую к стороне b и за h₃ высоту, проведённую к стороне c. Тогда 2S=ah₁=bh₂=ch₃. Так как в нашем случае a<b<c, то h₁>h₂>h₃. Значит, наибольшая высота - та, которая проведена к стороне, равной 4. Если сторона равна 4, а площадь равна 24, то из формулы площади треугольника легко найти высоту:
надо взять отрезок, равный 2 медианам, в качестве третьей стороны, и построить треугольник по 3 сторонам. В полученном треугольнике стороим медиану к стороне, равной удвоенной заданной медиане (то есть делим её пополам и середину соединяем с противоположной вершиной). Продлеваем полученную медиану за основание так, чтобы её длина удвоилась, и полученную точку соединяем с концами отрезка, который - удвоенная медиана, треугольник готов. И даже целых два :)))