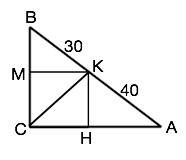
Все углы четырехугольника МКНС, вписанного в прямоугольный треугольник АВС – прямые, две стороны равны по условию, две другие им параллельны и противолежат, поэтому он – квадрат.
Его диагональ СМ для прямого угла С является биссектрисой.
Биссектриса угла треугольника делит противолежащую этому угла сторону на отрезки, пропорциональные прилежащим сторонам. ⇒
ВС:АС=ВК:АК.
Обозначим АС=х, ВС=у. ⇒
у:х=30:40 ⇒ у:х=3:4 ⇒
у=3х/4
АВ=30+40=7•10
По т.Пифагора
АВ²=АС²+ВС²=х²+у² Заменим у на его значение, выраженное через х:
7²•10²=х²+ 9х²/16
7²•10²=25x²/16
25x²=49•100•16
x²=49•4•16 ⇒x=7•2•4=56 см – длина АС
ВС=3•56/4=42 см
Вариант решения.
Площадь трапеции равна произведению высоты на полусумму оснований.
S=CH•(AD+BC):2
Проведем СЕ || ВD до пересечения с продолжением АD в точке Е. Противоположные стороны ВСЕD параллельны, он- параллелограмм, CE=BD, BC=DE.
Треугольник АСЕ - прямоугольный (СЕ║BD)
Его площадь равна СН•(AD+DE):2/ Нo DE=BC ⇒
Площадь треугольника АСЕ равна площади трапеции.
Площадь прямоугольного треугольника равна половине произведения катетов.
S=AC•BD:2=14•10:2=70 (ед. площади)
---------
Первое решение дано по формуле площади четырехугольника S=d1•d2•sinf, где f- угол между диагоналями.
Нахождение площади трапеции через площадь треугольника также нередко встречается в задачах. Оба решения желательно помнить.