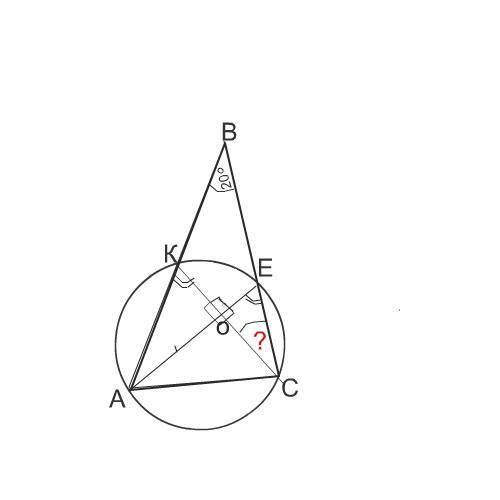
Сделаем рисунок к задаче.
Рассмотрим треугольники АКС и АЕС. Углы при К и Е в них равны, так как являются вписанными углами опирающимися на одну и ту же дугу, стягиваемую хордой АС.
Следовательно углы ВКС и ВЕА тоже равны как смежные с ними.
Угол КОЕ прямой по условию задачи.
Сумма углов четырехугольника равна 360°
Сумма равных углов ВКС и ВЕА равна
360-90-20=250°
Углы эти равны по 250:2=125°
Смежные с ними углы АЕС и АКС равны по 180-125= 55°
Сумма углов треугольника равна 180°
Так как угол ЕОС прямой, угол КСВ равен 180-90-55=35°
Объяснение:
Сумма смежных углов равна 180°
1)
а,б) если <АОВ больше <ВОС в 4р.
Пусть градусная мера угла <ВОС равно х. Тогда градусная мера угла <АОВ 4х
Составляем уравнение.
х+4х=180°
5х=180°
х=180/5
х=36° градусная мера угла <ВОС
<АОВ=4*36=144°
ответ: <АОВ=144°; <ВОС=36°
Если <АОВ меньше <ВОС, составляется такое же уравнение. При этом <АОВ=х; <ВОС=4х. <АОВ=36°; <АОВ=144°
2)
Пусть градусная мера угла <ВОС будет х;
Тогда градусная мера угла <АОВ будет (х+53°).
Составляем уравнение
х+(х+53)=180
2х=180-53
х=127/2
х=63,5° градусная мера угла <ВОС
63,5+53=116,5° градусная мера угла <АОВ.
ответ: 63,5°; 116,5°