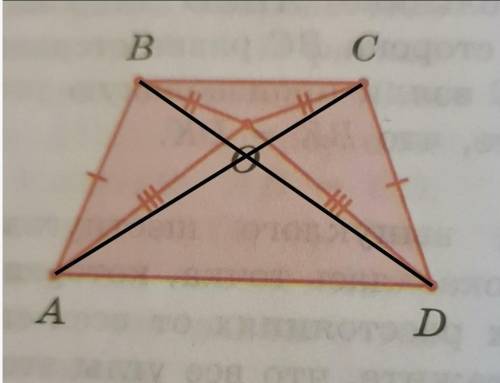
Рассмотрим ∆BOA и ∆COD.
BO=CO по условию;
AB=CD по условию;
АО=DO по условию;
Следовательно ∆ВОА=∆COD по трём сторонам.
Исходя из равенства: угол АВО=угол DCO как соответственные углы равных треугольников. Пусть каждый из этих углов равен х.
Так как ВО=СO, то ∆ВОС – равнобедренный с основанием ВС.
Углы при основании равнобедренного треугольника равны, то есть угол СВО=угол ВСО.
Пусть каждый из них равен z.
Угол АВС=угол АВО+угол СВО=х+z;
Угол DCB=угол DCO+угол ВСО=х+z;
Получим что угол АВС=угол DCB.
Рассмотрим ∆АВС и ∆DCB.
ВС – общая сторона;
Угол АВС=угол DCB (доказано ранее)
АВ=CD по условию;
Следовательно ∆АВС=∆DCB по двум сторонам и углу между ними.
Значит АС=BD как соответственные стороны равных треугольников.
Доказано.
Дано:
BC=7
AD=17
Угол при меньшем основании = 135⁰
Угол при меньшем основании 135⁰, тогда при большем 45⁰
Опустим высоту и получим равнобедренный треугольник
Вычислим высоту:
(17-7)/2=5
Вычислим площадь:
S=(17+7)/2×5=60
S=60
ответ: площадь трапеции 60 см²
Объяснение:
т.к. угол при меньшем основании равен 135, тогда при большем основании угол равен 45
Опускаем высоту из меньшего основания на большее и получаем прямоугольный треугольник, т.к. угол равен 45 градусов, тогда и второй 45 градусов. Получается это равнобедренный прямоугольный треугольник.
Часть, которую отсекла высота у большего основания будет (17-7)/2=5. Это равнобедренный треугольник следовательно и высота будет 5
Sтрап=(а+б)/2 * h где а и б - основания
S= (7+17)/2 * 5
S=60
ответ: S= 60
Дано: S=24cм^2
<A=30
1сторона-Х
2-ая сторона-3Х
S=absinA
3х*х*sin30=24
3x^2*sin30=24
x^2sin30=8
sin30=1/2
1/2(x^2)=8
x^2=16
x=4
3x=3*4=12
P=2(a+b)
P=2(4+12)=32
P=32см