3√34 см
Объяснение:
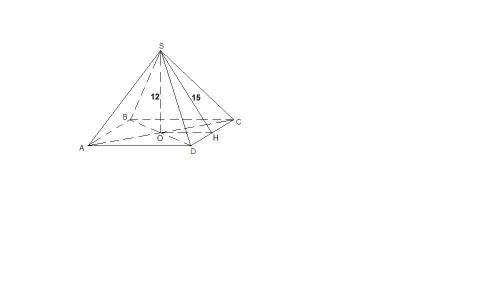
Пирамида правильная, значит в основании лежит квадрат, боковые грани - равные равнобедренные треугольники и высота проецируется в центр основания.
SO = 12 см - высота пирамиды,
SH = 15 см - апофема (высота боковой грани)
ΔSOH: ∠SOH = 90°, по теореме Пифагора
ОН = √(SH² - SO²) = √(15² - 12²) = √(225 - 144) = √81 = 9 см
ОН = 1/2 AD как средняя линия треугольника ACD.
DH так же половина стороны квадрата, поэтому
DH = OH = 9 см
ΔSHD: ∠SHD = 90°, по теореме Пифагора
SD = √(SH² + DH²) = √(225 + 81) = √306 = 3√34 см
V = Sосн*h.
Найдем площадь основания и высоту.
В основании куба лежит ромб со сторонами 12 см и углом равеным 60 градусов.
Площадь ромба равна:
S = 12*12*sin60° = 144*√3/2 = 72√3.
Площадь основания призмы вычисляется по формуле поиска площади ромба:
S=a2*sinα.
Меньшее из диагональных сечений является квадратом.
Сечение будет содержать меньшую из диагоналей ромба BD. BD<AC, так как ∠А=60°, а угол D=120 градусов ((360 - 60*2) * ½ = 120).
Значит, сечение BB1D1D - квадрат.
Найдем BD.
Из треугольника ABD: что угол А равен 60 градусов. Значит, два другие угла при основании тоже по 60 градусов ((180 - 60)*½ = 60).
Значит треугольник ABD равносторонний, ⇒ BB1 = BD = AD = 12, ⇒ h =12.
Найдем объем призмы:
V = 72√3 * 12 = 864√3 (см^3).
ответ: 864√3 см^3