Відповідь:
Пояснення:
1. ΔDBA=ΔACD; ΔABE=ΔECD
2. ∠1= ∠EAB+∠ABE
∠1= 20°+90°=110°
3. равнобедренный
4. ∠3= (180°-∠AED)/2
∠3= (180°-110°)/2=70°/2=35°
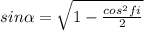
Ptkem = 16 см.
Объяснение:
В условии допущена описка.Площадь измеряется в кавдратных единицах, следовательно, площадь грани тетраэдра равна
S = 16√3 см².
Тетраэдр называется правильным, если все его грани - равносторонние треугольники. Тогда сторону тетраэдра найдем из формулы площади правильного треугольника:
S = (√3/4)*a², где а - сторона треугольника.
а² = 4*S/√3 = 4*16√3/√3 = 64 см² => a = 8см.
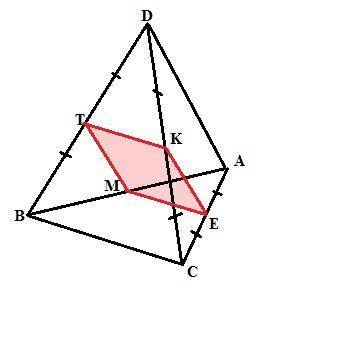
Точки T,K, и Е - середины ребер DB, DC и AC соответственно, следовательно, отрезки ТК и КЕ - средние линии треугольников - граней тетраэдра BDC и СDA и равны половинам сторон ВС и AD.
Построим сечение тетраэдра плоскостью ТКЕ. Плоскость BDC пересекается плоскостью TKE по линии ТК, параллельной прямой ВС. Но прямая ВС принадлежит и плоскости АВС. Следовательно, плоскость АВС пересечется плоскостью ТКЕ, проходящей через точку Е по прямой ЕМ, параллельной прямой ВС, а отрезок ЕМ является средней линией треугольника АВС. ЕМ = 4см. Соединив точки Т и М (середины сторон АВ и BD), получим сечение тетраэдра плоскостью ТКЕ - четырехугольник ТКЕМ, все стороны которого равны между собой и равны 4 см.
Периметр сечения Ptkem = 4*4 = 16 см.
1.
Равные треугольники ACD и DBA (АB=CD, угол B = угол С, сторона AD - общая)
2.
Чтобы вычислить градусную меру 1 рассмотрим сначала треугольник АВЕ
угол А = 20°, угол В = 90°, угол Е = (180-(90+20))=70°
Угол 1 смежный с углом Е. Сумма смежных углов = 180°
Угол 1 = 180-70=110°
3. Треугольник АЕD является равнобедренным
АЕ = ED
4.
Мы установили, что треугольник AED - равнобедренный
=> углы при основании равны
Так как угол 1 = 110°, то сумма двух других углов = 70° (180-110=70)
Угол 3 = 70:2 = 35°