ответ: АН=6/√2см
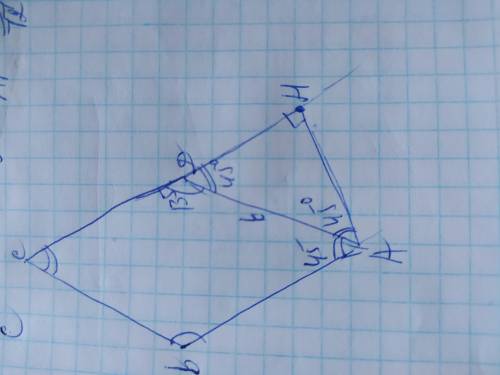
Объяснение: Обозначим вершины ромба А В С Д. Так как его периметр=24см, то его сторона=24÷4=6см. Пусть острый угол ромба=х, тогда тупой=3х. Зная, что сумма прилегающих углов ромба составляет 180°, составим уравнение:
х+3х=180
4х=180
х=180÷4
х=45
Итак: угол А=углу С=45°, тогда
угол В=углу Д=45×3=135°.
Продлим прямую СД и проведём к ней из вершины А высоту АН. Получился прямоугольный треугольник АДН, в котором АН и ДН - катеты, а АД гипотенуза,
угол Н=90°. Так как прямая СД параллельна АВ, то угол А=углуАДН=45°
Если в прямоугольном треугольнике один из острых углов составляет 45°, то второй угол ДАН=45°. Этот треугольник равнобедренный АН=ДН, поэтому каждый катет равен гипотенузе/√2, поэтому АН=ДН=6/√2см
2. Неверно - один из неизвестных углов может быть тупым
рассмотрим два случая, например, с углом в 40*
а) угол в 40* находится при основании, тогда:
второй угол при основании тоже 40*
угол напротив основания:
180-40*20=100* он тупой(больше 90*)
б) угол в 40* находится напротив основания, тогда:
углы при основании равны:
(180-40)/2=70*
3.Неверно - вписанный угол в два раза меньше центрального, опирающегося на ту же дугу.
4.Неверно - центром окружности, описанной около прямоугольного треугольника, является середина гипотенузы.
5. Неверно - потому что в ромбе может не соблюдаться основное условие:
около выпуклого четырёхугольника можно описать окружность только тогда, когда сумма его противоположных углов равна 180°.
6. Неверно - только если это не квадрат, только в этом прямоугольнике стороны будут касаться окружности.
7. Верно - в параллелограмме противоположные углы равны, а сумма углов при одной какой то стороне равна 180*.