ответ: 27 кв см
Условие задачи:
Периметр правильного треугольника, вписанного в окружность, равен 27 см. Найдите периметр и площадь правильного четырехугольника, описанного около этой же окружности.
Объяснение:
Найдем для начала, радиус вписанной окружности.
S=p*r, где полупериметр р=27/2= 13,5 см, а радиус r - нужно найти.
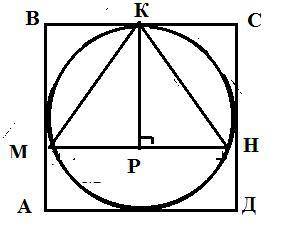
У правильного треугольника все стороны равны между собой а углы равны 60° . Так что медиана, КР является и биссектрисой и высотой. Любая сторона равна 27/3 = 9 см, следовательно из треугольника КРН
по определению косинуса
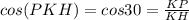
Отсюда КР = КН* cos 30 = 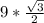
Значит площадь треугольника равна
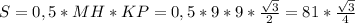
Значит 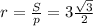
Из рисунка очевидно, что сторона квадрата равна диаметру окружности, то есть
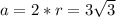
Площадь квадрата равна
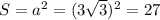 кв см
кв см
Смежный с ним будет 180-40=140. И два оставшиеся - вертикальные.
ответ: 40, 140, 40, 140.
2. Если сумма углов первой пары составляет 2/3 суммы другой пары, то соответственно, сумма второй пары составляет 3/2 суммы первой.
За х обозначим сумму первой пары. Тогда 3х/2 - сумма второй пары.
Опять-таки сумма всех 4 углов равна х+3х/2=5х/2=360. Отсюда 5х=720, значит х=144. Значит один из этих вертикальных равен 72.
Ему смежный 108.
ответ: 72, 108, 72, 108.