Правильная пирамида — это пирамида, основанием которой является правильный многоугольник, а вершина пирамиды проецируется в центр этого многоугольника.
Диагонали, проведенные через центр основания данной пирамиды, делят его на 6 правильных треугольников со стороной 3 см.
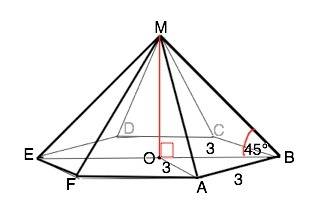
Обозначим пирамиду ABCDEF, центр - О.
Высота МО и половина ВО диагонали ВЕ образуют прямоугольный треугольник МОВ, острый угол МВО=45°. ⇒ Это равнобедренный треугольник, и МО=ВО=3 см.
Объём пирамиды равен 1/3 произведения высоты на площадь основания.
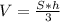
Площадь правильного шестиугольника – сумма площадей 6 правильных треугольников, площадь которых найдем по формуле:
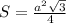
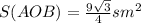
Площадь основания
6•9√3/4 sm²
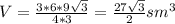
Объяснение:
1. Сумма углов выпуклого многоугольника равна 180°*(n-1), где n -
количество углов выпуклого многоугольника.
S=180°*(7-2)=180°*5=900°.
2. S=6*7=42 (cм²).
3. S=180°*(13-2)=180°*11=1980°.
4. 15*7=105 (cм²).
5. S=ah/2 h=2S/a=2*45/18=90/18=5 (cм).
6. (1/2) основания = √(15²-9²)=√(225-81)=√144=12 (см).
S=12*9=108 (cм²).
7. Пусть меньшая диагональ - х. ⇒
Большая диагональ - х+8.
24+8=32 (см). ⇒
S=(24*32)/2=12*32=384 (cм²).
8. S=10*9,5=95 (дм²) s=0,5²=0,25 (дм²) ⇒
N=95/0,25=380 (квадратов).