Тут, наверное, площадь поверхности шара, которая равна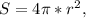 
где r - радиус шара. Остается только найти r. Пусть сторона куба равна а. Тогда 
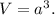По условию задачи V=125. Тогда 
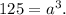Тогда а=5. Теперь можно рассмотреть сечение куба, где у шара будет свой диаметр. В сечении получаем квадрат со стороной 5, внутрь которого вписана окружность. Очевидно, что диаметр этой окружности совпадает с длиной стороны квадрата, то есть d=5. d=2r, 2r=5, r=2,5. Подставим в вышеуказанную формулу.
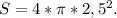
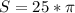
Если хотите приближенно.
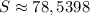
Очень подробно.
Треугольники AOD и BOC подобны по свойству трапеции.
Площади подобных треугольников относятся, как квадраты коэффициента их подобия
25:16=k²
k=√(25:16)=5:4
Следовательно, основания трапеции относятся, как 5:4
Обозначим
высоту ᐃ ВОС=h₁
высоту ᐃ АОD=h₂
S АОD=h₂·АD:2
S ВОС=h₁·ВС:2
Площадь трапеции равна произведению ее высоты на полусумму оснований:
Высота трапеции Н
S ABCD=Н·(АD+ВС):2
Н=h₂+h₁
S ABCD =(h₁+h₂)·(АD+ВС):2=
=h₁·АD+h₂·АD+h1·ВС+h₂·ВС
1)
Применим свойство пропорции: произведение средних членов пропорции равно произведению крайних.
h₂:h₁=5:4
4h₂=5h₁
h₂=5h₁/4
S AOD=h₂·АD:2=5h₁/4·АD:2
25=5h₁/4·АD:2 Умножим на два обе части уравнения
12,5=5h₁/4·АD
5h₁/4 =12,5:AD
h₁:4=2,5:AD
h₁·AD= 4·2,5 =10 см²
Т.к. площади боковых треугольников у трапеции равны равны, то h₂·ВС=10 см²
Проверим это:
2)
h₂:h₁=5:4
5h₁=4h₂
h₁=4h₂/5
S ВОС=h₁·ВС:2=4h₂/5·ВС:2
16=4h₂/5·ВС:2 Умножим на два обе части уравнения
8=4h₂/5·ВС
4h₂:5=8:ВС
4h₂·ВС=8·5=40
h₂·ВС=40:4=10 см²
3) Подставим значения h₂·ВС и h₁·AD в уравнение площади трапеции
S ABCD=h₁·АD+25+16+h₂ВС=41+=h₁·АD+h₂·ВС =
S ABCD=10+25+16+10= 61 см
1.сумма смежных углов =18Вертикальные0градусов.
Пусть один угол будет равен Х,
тогда второй угол будет равен( х+30)
Составим уравнение:
Х+( х+30)=180°
х+х+30=180
2х+30=180
2х=180-30
2х=150
х=75
Второй угол будет равен:
Х+30=75+30=105
ответ:75°,105°
2 Поскольку вертикальные углы равны,а у нас их два. то можно составить такое уравнерие:
Х+Х=98
2х=98
Х=49
ответ: 49°
Объяснение:
Или можно просто 98:2=49°