Question

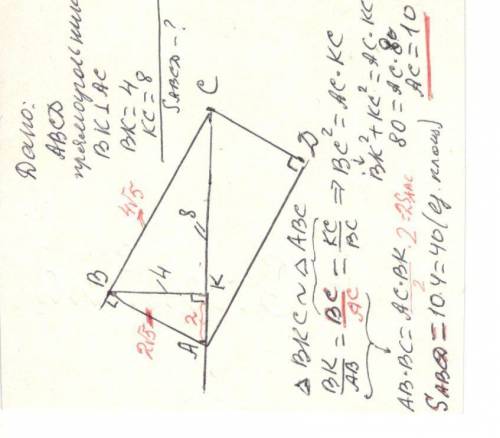
В прямоугольнике ABCD из вершины B опущен перпендикуляр BK на диаганаль AC. Найдите площадь прямоугольника, если BK = 4 , KC= 8

Answer 1

ответ: 40 (ед. площади)

Объяснение: Задачу можно решить разными Вот один из них.

  Диагональ прямоугольника делит его на два равных прямоугольных треугольника.

Треугольник АВС - прямоугольный. ВК - перпендикулярна АС.⇒ ВК - высота ∆ АВС.

  Высота прямоугольного треугольника делит его на треугольники, подобные между собой и исходному.

Из подобия ⊿АВК и⊿ВКС следует ВК:АК=КС:ВК ⇒

ВК²=АК•КС

16=8 АК ⇒

АК=2.

АС=АК+КС=2+8=10

 Площадь треугольника равна половине произведения высоты на сторону, к которой проведена.

Ѕ(АВС)=0,5•ВК•АС =0,5•4•10=20

S(ABCD)=2•Ѕ(АВС)=2•20=40 (ед. площади)

Answer 2

В прямоугольнике ABCD из вершины B опущен перпендикуляр BK на диагональ AC. Найдите площадь прямоугольника, если BK = 4 , KC= 8    

"Решение"

* * * Cразу можно  написать:  BC² = AC *KC _ пропорциональные отрезки в прямоугольном треугольнике  * * *   A  если . . .

ΔBKC ~ΔABC  ⇒ BK/AB  =    BC / AC = KC/BC ⇔  BC² = AC *KC , но

BC² = BK²+ KC² =4² +8² =80 (теорема Пифагора)

80 =AC*8 ⇒AC =10    

BK/AB = BC / AC ⇔  AB *BC = AC*BK ⇔ S(ABCD) = AC*BK =10*4= 40                        (ед. площади)        ||  S(ABCD) =2*AC*BK/2 =2S(ABC) ||

S(ABCD)  = AC*BK =10*4= 40   (ед. площади)