ответ: h=5 см .
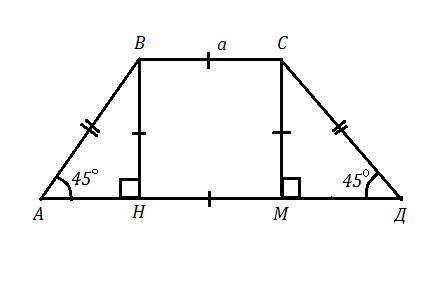
АВСД - трапеция, АВ=СД , ∠А=∠Д=45° ,
ВС=а , ВН ⊥ АД , h=ВН=ВС=а , S(трап)=50см² .
Опусти перпендикуляр из вершины С на АД: СМ ⊥ АД .
Тогда ВСМН - прямоугольник , противоположные стороны которого равны, ВС=МН и ВН=СМ , но так как по условию ВС=ВН, то ВСМН - квадрат, сторону которого обозначим "а" .
ΔАВН - прямоугольный, с углом ∠А=45° . Тогда и ∠АВН=90°-45°=45° .
То есть ΔАВН - равнобедренный и АН=ВН=а .
Аналогично, из ΔСДМ получаем, что ДМ=СМ=а .
Тогда АД=АН+НМ+МД=а+а+а=3а .
Площадь трапеции : 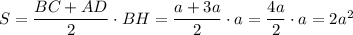
По условию: 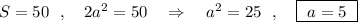
нормаль от плоскости oxy будем иметь координаты n(0;0;1)
1 - произвольное число, нормально может быть сколь угодно длинной в высоту
вектор MN(4-3;6-6;2-1)=MN(1;0;1)