Объяснение:
3) По теореме Пифагора
АВ²=АС²+СВ²
АВ²=35²+12²
АВ=√(1225+144)=√1369
АВ=37 см
Квадрат катета =произведению гипотенузы на проекцию этого катета
СВ²=АВ*DB
12²=37*DB
DB=144÷37=3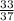
,AD=37-3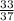=33
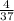
Квадрат высоты = произведению проекций этих катетов
CD²=DB*AD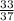=3*33=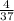
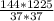, CD=√(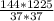)=12*35/37=420/37
8)AB=2+18=20 м
Квадрат высоты = произведению проекций этих катетов
CD²=AD*DB=2*18=36
CD=6 м
Квадрат катета =произведению гипотенузы на проекцию этого катета
AC²=AD*AB, АС=√(2*20)=2√10
По т. Пифагора
АВ²=АС²+АВ², СВ²=АВ²-АС²
СВ²=20²-(2√10)² , СВ=√(400-40)=√360=6√10
Объяснение:
У даному випадку ми можемо використати теорему Піфагора для знаходження сторони АВ трикутника АВС. За теоремою Піфагора, квадрат гіпотенузи (сторона протилежна прямому куту) дорівнює сумі квадратів катетів (інших двох сторін, що прилягають до прямого кута).
У нашому випадку, кут С = 90 градусів, тому СВ є гіпотенузою, а АС і АВ є катетами. Ми знаємо, що МС перпендикулярна трикутнику АВС, тому МС є висотою, яка розділяє гіпотенузу СВ на дві частини у співвідношенні 7:8. Тому ми можемо скласти рівняння:
(МС/СВ) = (АС/АВ) = 7/8
Також нам відомо, що кут А = 30 градусів, тому кут САМ (де М - середина СВ) дорівнює 60 градусів.
За до трикутника САМ ми можемо обчислити сторону АС:
tan(60 градусів) = АМ/МС
АМ = МС * tan(60 градусів)
АМ = 8 см * √3
АМ = 8√3 см
Тепер ми можемо скористатися співвідношенням сторін:
(АС/АВ) = 7/8
АС/АВ = 7/8
АС = 8√3 см (знайдено раніше)
АВ = АС * (8/7)
АВ = (8√3 см) * (8/7)
АВ = 64√3/7 см
Таким чином, довжина АВ становить 64√3/7 см.
Диагональ прямоугольника является диаметром описаной вокруг него окружности. Если r=8, то d=2r=2×8=16 см. Диаметр окружности 16 см
Диагональ прямоугольника 16 см