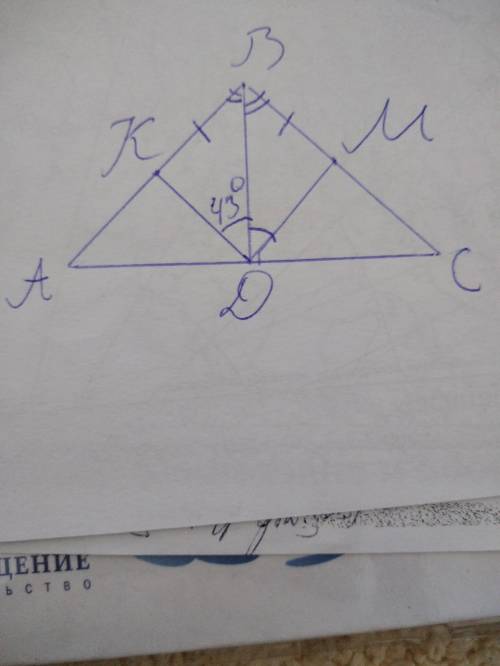
Рѣшеніе:
Рассмотрим треугольники КВD и BMD:
1). Сторона BD общая
2). Т.к. ВС=АС, а точки К и М делят их пополам, то ВК=ВМ.
3). ВD медиана, но в равнобедренных треугольниках медианы, проведённые к основанию являются и высотами и биссектрисами тоже. А значит ВD — биссектриса угла В, => углы МВD и KBD равны.
Из всего выше перечисленного следует, что треугольники KBD и BMD равны по 1 признаку равенства треугольников, значит все их элементы совпадают, значит угол КDB и MDB равны => угол МDB=43°
Отвѣтъ: угол МDB=43°.
(а + b) / 2 = 10
где a, b - верхнее и нижнее основания
откуда получаем:
a + b = 20
а = 20 - b
2. Находим площадь S₁ верхней части трапеции, которая по условию составляет 3 части
S₁ = (10+а)/2 * h
Находим площадь S₂ нижней части трапеции, которая по условию составляет 5 частей
S₂ = (10 + b) /2 h
h - высота каждой из вышеуказанных трапеций, которая равна половине высоты данной основной трапеции.
3. Получаем пропорцию
S₁ : S₂ = 3 : 5
Подставив вместо S₁ и S₂ их выражения, имеем
(10+а)/2 * h : (10 + b) /2 h = 3 : 5
Сократив, имеем
(10 + a) * 5 = (10 + b) *3
Подставляем вместо а выражение а = 20 - b
(10 + 20 - b) *5 = (10 + b) *3
(30 - b) * 5 = 30 + 3b
150 - 5b = 30 + 3b
5b + 3b = 150 - 30
8b = 120
b = 120 : 8
b = 15 - нижнее основание
а = 20 - b
а = 20 - 15 = 5
a = 5 - верхнее основание
ответ: а = 5; b = 20