1Точка С лежит между точками А и В. Найдите длину отрезка АС, если АВ=8,5 см,
ВС=4,6 см.
2Биссектриса ВС угла АВD разбивает его на два угла, один из которых равен 250.
Найдите величину угла АВD.
3Один из смежных углов равен 114градусов. Найдите величину второго.
4. На рисунке ‖. одиниз углов равен 115градусов
5. Найдите периметр равнобедренного треугольника, боковая сторона которого 6 см, а
основание 4см.
6. На рисунке отрезок МК параллелен стороне АС. Луч MN является биссектрисой угла
ВМК. Найдите величину угла MNK.
7. В равнобедренном треугольнике АВС с основанием АС проведены биссектрисы АЕ и
СД. Докажите, что треугольник АДС равен треугольнику СЕА.
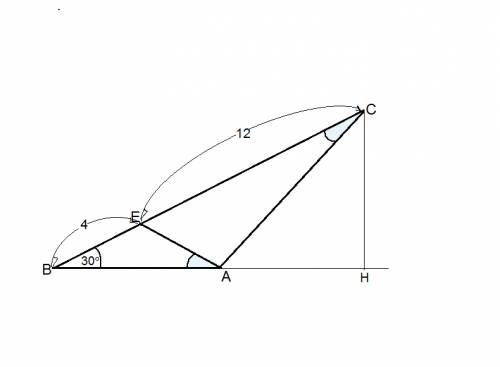
8. В прямоугольном треугольнике острый угол относится к внешнему, не смежному с ним
и с прямым углом как 1:4. Найдите острые углы треугольника и его гипотенузу, если
катет, лежащий напротив наименьшего острого угла равен 12 см.
Вот такое нахальное решение. Ну уж простите :)
Пусть катеты a и b, гипотенуза с. Я строю квадрат со сторонами (a + b), и дальше обхожу все 4 стороны по часовой стрелке, откладывая отрезок а от вершины.
(Пояснение.
Построенный со стороной (a + b) с вершинами АBCD, А - "левая нижняя" вершина. От А вверх - вдоль АВ, откладывается а, потом от В вправо - вдоль ВС откладывается а, потом от С вниз, вдоль CD, откладывается а, и от D вдоль DA откладывается а.)
Все эти точки соединяются.
Получился квадрат со стороной с, вписанный в квадрат со стороной (a+b).
Ясно, что центры этих квадратов совпадают. Это автоматически доказывает то, что надо в задаче.
(Если не ясно, постройте там пару треугольников из диагоналей обоих квадратов и отрезков длины а и докажите их равенство.
На самом деле не надо ничего доказывать - эта фигура из двух квадратов переходит сама в себя при повороте вокруг центра большого квадрата на 90 градусов. Поэтому центр "вписанного" квадрата совпадает с центром большого, то есть лежит на биссктрисе прямого угла большого квадрата. Ну, и биссектрисе прямого угла исходного треугольника, само собой - это одно и то же. Этих треугольников там даже четыре, а не один :), можно любой выбрать за исходный.)