Дано: AD=DM=2, MABCD-пирамида, ABCD - квадрат
Найти: S(поверхности)-?, V-?
Для начала найдем объем. Общая формула V=1/3*S*h
h - высота, и это у нас DM, как видно на рисунке
S - площадь основания. площадь квадрата a^2, т.е. в нашем случае AD^2
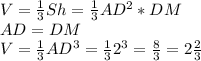
С площадью поверхности все сложнее
Она складывается из площади основания, площади треуг. MAB, площади треуг. MBC, площади треуг. MCD и площади треуг. MDA.
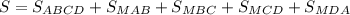
при этом заметим, что треугольники MDA и MCD равны, а также треугольнки MAB и MBC тоже равны, поэтому:
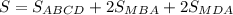
площадь основания, как и говорилось раньше, находится легко:
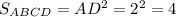
площадь треугольника MAB тоже довольно легко находится.
т.к. DM перпендикулярен DC, то и MA перпендикулярен AB
Это прямоугольный треугольник
Найдем AM, а затем сможем найти и площадь MBA
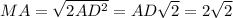
Площадь треугольника MBA
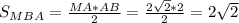
Площадь треугольника MDA находится ещё легче, прямоугольный теругольник, два катета известно:
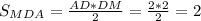
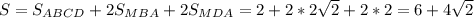
ответ: 6+4√2
Объяснение:
ΔАВС - равнобедренный, АВ = ВС
АС - основание, h = ВК - высота Δ- ка
О - центр вписанной окружности
(Центр вписанной в треугольник окружности является точкой пересечения его биссектрис. Поскольку в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с медианой и высотой, то центр вписанной в равнобедренный треугольник окружности лежит на высоте и медиане, проведенных к основанию).
Соединим т.О и т.С.
Т.к. ВК⊥ АС, то ΔОКС - прямоугольный.
ОС - биссектриса, поэтому ∠ОСК = 30°/2 = 15°
r /КС = tg 15° → r = KC * tg 15°
h = tg30°* KC
h - r = 2 по условию, поэтому
KC*tg30° - KC * tg 15° = 2
КС(tg30°- tg 15°) = 2
КС = 2 / (tg30°- tg 15°)
АС = 2КС = 4 / (tg30°- tg 15°)