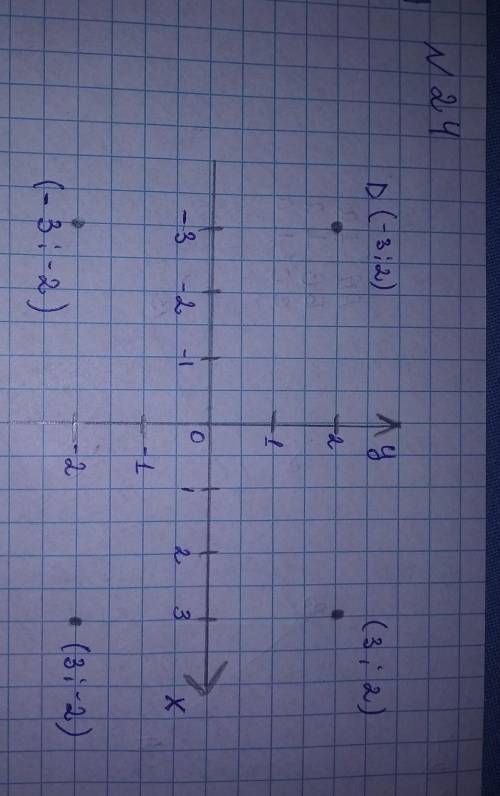
№24
а) точка симметричная относительно начала координат (3;-2)
б) точка симметричная относительно оси ОХ (-3;-2)
точка симметричная относительно оси ОУ (3;2)
(когда делаешь семетрию относительно
• начала координат нужно поменять знаки + на -, и - на + у: "х" и "у"
• оси ОХ знак нужно поменять только у: "у"
• оси ОУ знак нужно поменять только у: "х")
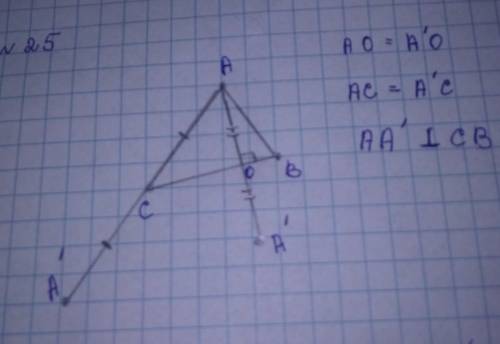
№25
а) симметрично относительно вершины С
нужно продлить сторону АС в направлении точки С в два раза и на конце мы получим точку А'
у нас получается прямая АА' и точка С которая делит эту прямую пополам
б) симметрично относительно стороны прямой ВС
проводим высоту из точки А до стороны ВС и обозначаем там точку О
дальше нужно продлить нашу высоту АО в 2 раза и в конце поставить точку А'
у нас будет прямая АА' которая перпендикулярная прямой ВС и точкой их пересечения делиться пополам
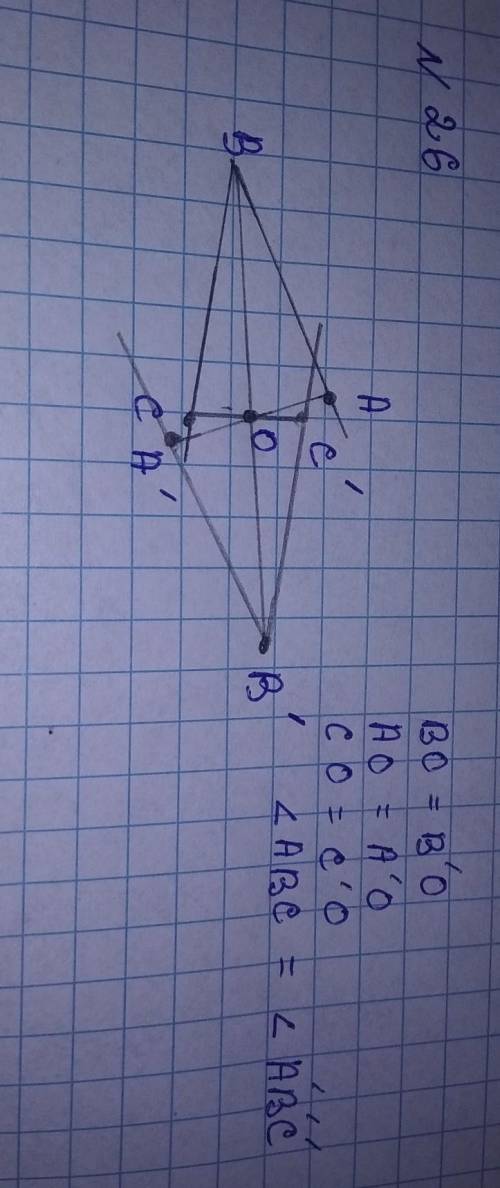
№26
из каждой точки угла проводим прямую до точки О
продолжу прямую в два раза так что точка О делит мои прямые пополам
и на них в соответствии ставлю точки А', В', С' и соединяю их по порядку
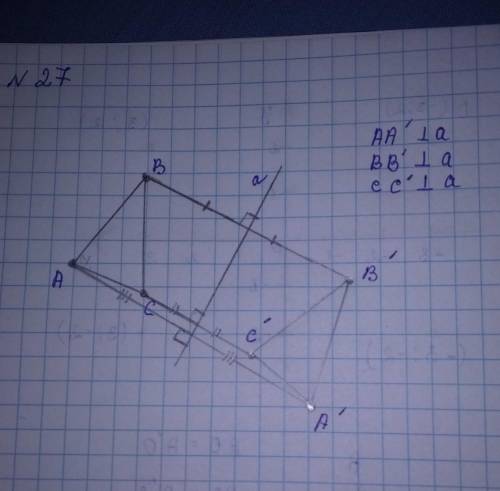
№27
из каждой вершины треугольника провожу перпендикуляр до прямой "а"
продолжу перпендикуляры в два раза и на их концах поставлю точки А', В', С' и соединяю их по порядку
(рисунки прикрепляю к каждому заданию)
надеюсь всё будет понятно
1. Используя теорему синусов, получим
8/(sin30°)=x/(sin45°),
8/0,5=х/(1/√2); х=16/√2=8√2
у/sin(180°-30°-45°)=8/0,5; у=16*sin105°=16*соs15°
2. Внешний угол при вершине R равен сумме двух внутренних, не смежных с ним, значит, внутренний угол М равен 80°-50°=30° По теореме синусов 13/sin30°=х/sin50°;
х=(13*sin50°)*2= 26*sin50°; QRM=180°-80°=100° по свойству смежных углов
у/sin100°=13/sin30°; у=2*13sin100°=26*sin100°
3. ∠МКТ=180°-60°-45°=75°
у/sin75°=20/sin60°; у=(20*sin75°)/(√3/2)=
(40√3/3)(0,5*√2/2+√√2*√3/(2*2))10√3(√2+√6)/3
х/=sin45°=20/sin60°; х*√3/2=20*√2/2; х= 20*√6/3
Угол между плоскостями АВС и АВD равен 60°, при этом DA⊥AB, CB⊥AB и АD = 2, АВ = 4, СВ = 3. Найдите CD.
Проведем ВК║DA и ВК = DA. Тогда ABKD - параллелограмм, и так как DA⊥AB - прямоугольник.
АВ⊥ВК, АВ⊥СВ, значит АВ⊥(СВК) и ∠СВК = 60° - линейный угол двугранного угла между плоскостями треугольников.
Так как отрезок АВ перпендикулярен плоскости СВК, то и плоскость АВС перпендикулярна плоскости СВК, поэтому перпендикуляр СН к плоскости АВС будет лежать в плоскости СВК.
ΔСВН: ∠СНВ = 90°, ∠СВН = 60°, ⇒ ∠ВСН = 30°, тогда
НВ = СВ/2 = 1,5
по теореме Пифагора:
СН = √(СВ² - ВН²) = √(9 - 9/4) = √(27/4) = 3√3/2
DK = AB = 4, КВ = AD = 2 как противоположные стороны прямоугольника,
КН = КВ - ВН = 2 - 1,5 = 0,5
ΔDKH: ∠DKH = 90°, по теореме Пифагора
DH = √(DK² + KH²) = √(16 + 1/4) = √(65/4) = √65/2
ΔCDH: ∠CHD = 90°, по теореме Пифагора
CD = √(CH² + DH²) = √(27/4 + 65/4) = √(96/4) = √23