По теореме Пифагора, если обозначить за х сторону квадрата, и вспомнить, что площадь квадрата можно еще посчитать как две площади прямоугольного треугольника, построенного на двух сторонах.
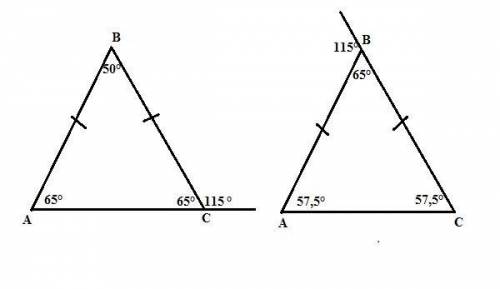
1. 65°, 65°, 50°.
2. 57,5°; 57,5°; 65°.
Объяснение:
Нам дан один из внешних углов равнобедренного треугольника. У равнобедренного треугольника углы при основании равны.
Значит возможны два варианта решения:
1. Если дан внешний угол при основании, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Тогда угол при вершине треугольника равен 180° - 2·65° = 50° (по сумме внутренних углов треугольника, равной 180°).
ответ: 65°, 65°, 50°.
2. Если дан внешний угол при вершине, то внутренний, смежный с ним, равен 180° - 115° = 65° (сумма смежных углов равна 180°).
Внешний угол треугольника равен сумме двух внутренних (в нашем случае равных), не смежных с ним углов. Следовательно, углы при основании такого треугольника равны 115°:2 = 57,5°.
ответ: 57,5°; 57,5°; 65°.
Обозначают так: точка отсчета, начало луча, к примеру А, вторая буква - это ближе к концу графического изображения луча, к примеру В. Луч АВ.
2.Углом называется часть плоскости ограниченная двумя лучами.
Сами лучи называются сторонами угла, а общая точка, из которой лучи выходят, называются вершиной угла.
3.Градусная мера, которого 180 градусов.
1) 0, 1, бесконечность
2) прямая, исходящая из одной точки, обозначение - маленькие буквы греческого алфавита
3) два луча, выходящих из одной точки
4) имеющие равные стороны и углы
5) по линейке (или другим подобным при
6) делящая отрезок на 2 равные части
7) транспортиром (или другим подобным при
8) луч, делящий угол на две равные части
линейка, циркуль, рулетка
9) Градус обозначается °. Один оборот равен 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
1 градус = 0,017453293 радиан
Объяснение:
1. рассмотрим прямоугольный треугольник, образованный смежными сторонами квадрата и его диагональю: d^2=a^2+a^2=2*a^2
2. S квадрата =a^2
3. (d^2)/S=(2*a^2)/(a^2)=2, площадь квадрата = половине квадрата длины его диагонали.