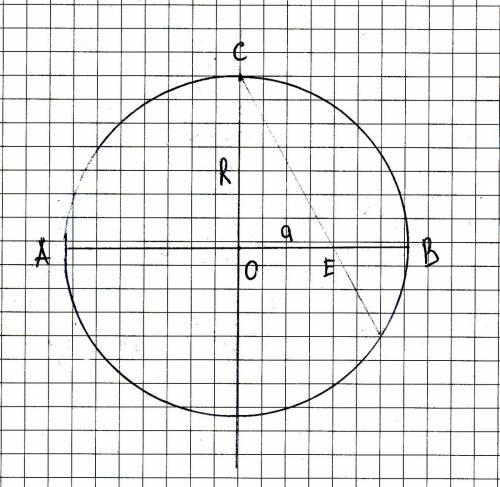
См. чертеж.
Прямые симметричны относительно ОС, поскольку усеченные круговые сегменты (один из них - СЕВ, ограничен дугой СВ) равны по площади, и оба равны четверти круга с вырезанным прямоугольным треугольником (справа это ОСЕ), следовательно, прямоугольные треугольники равны по площади, один катет у них общий, => они равны. Это - очевидно, но надо было это отметить.
Осталось понять, что 2*Scoe = Sceb = Socb - Scoe; :)
3*R*a/2 = pi*R^2/4;
ОЕ = а = pi*R/6; BE = R - a = R*(1 - pi/6);
Две прямые поделят диаметр на три отрезка
R*(1 - pi/6); pi*R/3; R*(1 - pi/6); ну, отсюда пропорция
(1 - pi/6) : (pi/3) : (1 - pi/6)
1) ΔAOC = ΔBOC по двум катетам (OC - общий, AO = OB т.к. O - середина AB) ⇒ CB = AC = 10
ответ: 10
2) В равнобедренном треугольнике углы при основании равны ⇒ ∠ABC = ∠ACB = (180 - 80)/2 = 50°
ответ: 50°
3) ∠CAB смежный с углом ∠BAK ⇒ ∠CAB = 180 - 120 = 60°
Рассмотрим ΔABC - прямоугольный
∠CAB = 60° ⇒ ∠ABC = 90 - 60 = 30°
Катет, лежащий напротив угла в 30° равен половине гипотенузы: AC = 1/2 AB
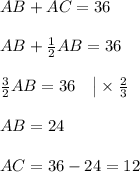
ответ: 12
4) В четырёхугольнике ABCD диагонали пересекаются и точкой пересечения делятся пополам ⇒ ABCD - параллелограмм
В параллелограмме сумма углов, прилежащих к одной стороне, равна 180°
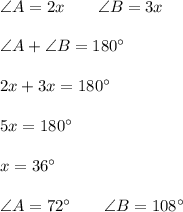
ответ: 72°

Чтобы определить равны ли векторы, нужно найти разницу координат концов и начал этих векторов. Если разница одинакова, то и векторы одинаковы. Начнем с вектора АВ. Конец вектора - есть его конечная точка, т.е. В. Координаты точки В - (2;3). Первая координата - значение х, вторая - значение у. Начало вектора АВ - есть точка А, которая тоже имеет определенные значения координат х и у. Теперь, чтобы найти разность, из значения координаты х конца вычитаем значение координаты х начала, т.е. -1-2=-3. Тоже делаем с у: 2-3=-1. Получили разницу (-3;-1). Теперь по той же схеме действуем с вектором СМ и получаем: -3-0=-3 и 0-1=-1. Полученная разница - (-3;-1). Разницы координат у векторов равны, следовательно, вектор АВ равен вектору СМ.