Точка D выбирается так, что
угол BDA = угол CBA; Обозначим его за Ф.
тогда в треугольниках АВС и ABD все углы попарно равны;
Сторона АВ в ABD соответствует стороне АС в АВС - это видно из соответствия углов и сторон;
Поэтому ABD имеет все линейные размеры в 3/2 раза больше (его стороны равны 3; 4,5; 6). То есть BD = 6.
Отсюда, кроме того, DC = 2,5.
Надо вычислить длину медианы DM в треугольнике BDC.
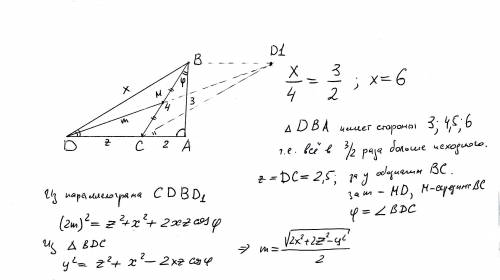
См чертеж. Из достроенного тр-ка CDD1 (СD1 II BD) по теореме косинусов
(2*m)^2 = x^2 + z^2 + 2*x*z*cosФ;
А из тр-ка BDC
y^2 = x^2 + z^2 - 2*x*z*cosФ; здесь y = ВС.
Складываем, и получаем выражение для квадрата медианы через квадраты сторон :)))
m^2 = (2*x^2 + 2*z^2 - y^2)/4; Подставляем x = 6, y = 4, z = 2,5.
получаем
m = корень(30)*3/4
Я добавил чертеж, поясняющий, как строится треугольник BDA
1. ΔABC-правильный . R и r-радиусы вписанной и описанной окружностей. Выразите R через r.
a₃ = 2r√3 и a₃ = R√3 ⇒ 2r√3= R√3 , R=2r.
4. Найдите площадь равностороннего треугольника, вокруг которого описано окружность радиуса 3 см.
a₃ = R√3 ⇒ a₃ = 3√3 см
S(равностороннего треуг.)=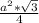
⇒ S(равн.треуг.)= 
= 
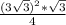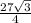(cм²)
5. Определите количество сторон правильного многоугольника углы которого равны 160 градусов.
Многоугольник правильный , поэтому сумма всех внутренних углов 160*n .
160*n=180(n-2) , 160n=180n-360 , 20n=360 , n=18. Количество сторон 18.
((n-2)/n*180- формула для нахождения углов в правильном многоугольнике )
6. В правильный треугольник ,сторона которого 4√3 cм, вписана окружность. Вокруг окружности описан квадрат. Найдите сторону квадрата.
a₃ = 2r√3 , 4√3= 2r√3 ⇒ r=2 см.
Квадрат описан около окружности, значит сторона квадрата равна
a₄ =2r или a₄ =4см.