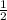 АС=[tex] \frac{1}{2} *6=3 см;
АС=[tex] \frac{1}{2} *6=3 см;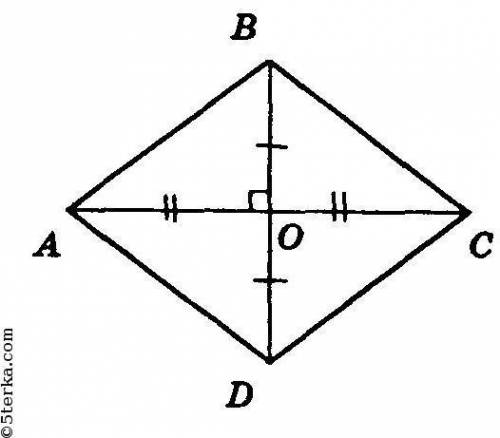
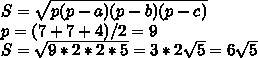
Радиус вписанной окружности равен половине высоты этой трапеции (высота равна диаметру. )
В трапецию можно вписать окружность, если суммы ее противоположных сторон равны.
8+18=26 - сумма боковых сторон
26:2=13 - боковая сторона.
Опустим из тупого угла высоту на большее основание.
Получим прямоугольный треугольник с гипотенузой 13, катетом, равным полуразности оснований и равным (18-8):2, и вторым катетом - высотой трапеции.
По теореме Пифагора диаметр окружности равен
√(13²-5²)=12см
Радиус равен половине диаметра
12:2=6 см
ответ: радиус вписанной окружности в трапцию равен 6 см
Координаты центра равны
х=(х(точки А)+х(точки В))/2
х=(3+5)/2=8/2=4
у=(у(точки А)+у(точки В))/2
у=(7+(-1))/2=6/2=3
координаты центра (4;3)
r - радиус
r^2=(x(точки А)-x(центра))^2+(y(точки А)-у(центра))^2
r^2=1+16
r^2=17
P.S. ^2 означает "в квадрате"