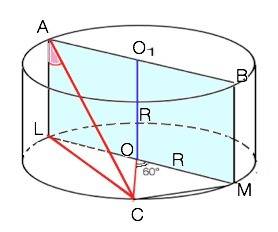
В равнобедренном ∆ СОМ ( радиусы СО=МО), центральный угол СОМ равен дуге СМ=60°. => угол ОМС=углу ОСМ=60°
В ∆ LMC вписанный угол С=90° ( опирается на диаметр LM).
LM=2R =>
LC=LM•sinOMC=2R•√3/2=R√3
Прямая АС и ось цилиндра лежат в разных плоскостях и не пересекаются. Они скрещивающиеся.
Чтобы найти угол между скрещивающимися прямыми, нужно:
провести прямую, параллельную одной из двух скрещивающихся прямых так, чтобы она пересекала вторую прямую. При этом получатся пересекающиеся прямые. Угол между ними равен углу между исходными скрещивающимися.
Образующая АL =R (по условию), параллельна оси цилиндра ОО1 и пересекается с прямой АС в точке А. =>
Угол LАС - искомый.
tg∠LАC=LC:AL=R√3/R=√3 – это тангенс 60°
Угол между прямой АС и осью цилиндра равен 60°
Прямые МВ и CD - скрещивающиеся по определению.
Прямые АВ и CD - параллельны, как противоположные стороны квадрата (основания). Следовательно, искомый угол между прямыми МВ и CD - это угол между скрещивающимися прямыми АВ и МВ -
угол ABM.
Проведем высоту боковой грани (апофему) МН.
Cos(<ABM)= HB/MH.
НВ = (1/2)*а, где "а" - сторона основания.
АО = (1/2)*d, где "d" - диагональ основания.
d = a*√2. AO= a*√2/2.
Высота пирамиды MO = АО*tg30 = (a*√2/2)*(√3/3) = a*√6/6.
Из прямоугольного треугольника МОН по Пифагору:
МН=√(МО²+ОН²) = √(а²*6/36+а²/4) = (а*√15)/6.
Тогда Cos(<ABM)= (а/2)/((а*√15)/6) = 3/√15 = √15/5.
ответ: Cos(<ABM)= √15/5 ≈ 0,7746.