очень Рассмотрите рисунки. Найдите обозначения равных элементов в треугольниках. Определите, на каком рисунке треугольники равны по II признаку равенства треугольников.
ответ:
2. На каком рисунке недостаточно равных элементов для применения признаков равенства треугольников?
ответ:
3. Какие равные элементы необходимо добавить, чтобы треугольники на этом рисунке были равны по I признаку равенства?
ответ:
4. Выберите неверное утверждение:
1) В равных треугольниках все соответственные стороны попарно равны.
2) Если две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника, то такие треугольники равны.
3) В равнобедренном треугольнике углы при основании равны.
5. Выберите верное утверждение:
1) В равнобедренном треугольнике медианы являются его биссектрисами и высотами.
2) В равнобедренном треугольнике все углы равны.
3) Если три стороны одного треугольника равны трём сторонам другого треугольника, то такие треугольники равны.
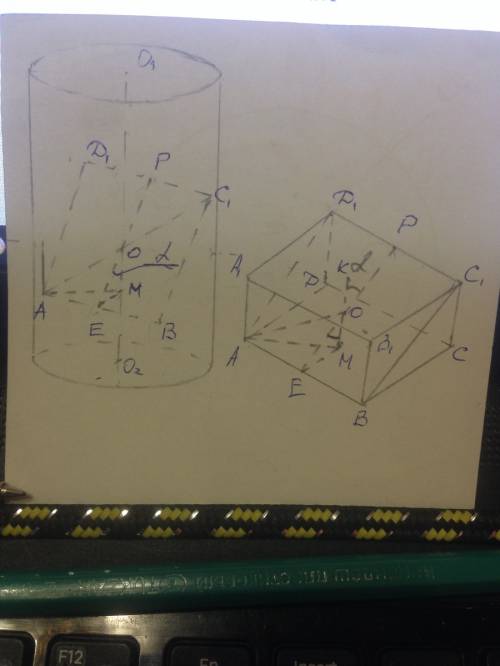
Расстояние от прямой DC до плоскости α - это перпендикуляр из любой точки этой прямой на плоскость α.
Итак, в прямоугольном треугольнике АЕD катет АЕ равен по Пифагору
АЕ=√(AD²-DE²)=√(36²-18²)=18√3.
Угол между двумя пересекающимися плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения. То есть угол между плоскостью α и плоскостью квадрата - это угол EAD, cинус которого равен отношению противолежащего катета к гипотенузе: Sinβ=ED/AD=18/36=1/2. Значит угол между плоскостями равен 30°.
Площадь проекции квадрата на плоскость α - это площадь прямоугольника AEFB, равная S=AB*AE=36*18√3=648√3см²