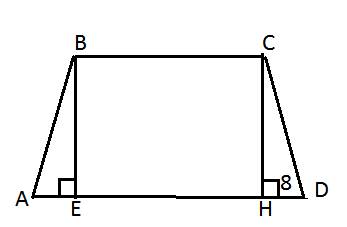
Биссектрисы двух внешних углов и внутреннего угла треугольника пересекаются в центре вневписанной окружности.
Центр вписанной окружности треугольника (I) является точкой пересечения биссектрис, AI - биссектриса ∠BAC
△BAI=△DAI (по двум сторонам и углу между ними)
∠BIF=∠DIF (смежные с равными)
AF - биссектриса внешнего угла ∠BID треугольника BEI
EF - биссектриса внутреннего угла ∠BEI
F - центр вневписанной окружности △BEI
BA - биссектриса внутреннего угла ∠EBI треугольника BEI
A - центр вневписанной окружности △BEI
Периметр первого основания равен р1=6+5+5=16. Треугольники оснований подобны с коэффициентом подобия р1/р2=16/32=1/2. То есть р2=2*р1. Отсюда-стороны большего основания вдвое больше и равны 12,10,10. Найдём площадь меньшего основания S=1/2*6*4=12, где 6 -основание, 4 -высота равнобедренного треугольника основания найденная по теореме Пифагора Н=корень из(5 квадрат-3 квадрат)=4. Отношение площадей подобных треугольников равно квадрату коэффициента подобия то есть S2=4S1=4*12=48. Объём усечённой пирамиды находим по формуле V=1/3*H*((S1+корень из(S1*S2)+S2))=1/3*4*(12+24+48)=112.