Из прямоугольного треугольника ABD
AD^2=AB^2+BD^2=9+16=25
AD=5
Площадь основания равна 2*площадь ABD=2*(3*4/2)=3*4=12
AD параллельно BC, следовательно параллельно B1C1, поэтому AD принадлежит плоскости AB1C1, и это прямая пересечения плоскости основания с плоскостью AB1C1
Пусть BE высота в треугольнике ABD
Тогда угол B1EB это угол между плоскостью основания и плоскостью AB1C1, так как BE перпендикулярно AD, B1E перпендикулярно AD по теореме о трёх перпендикулярах.
Треугольник B1EB -- прямоугольный треугольник с углом 45 градусов, а следовательно, равнобедренный прямоугольный треугольник, поэтому B1B=BE
Чтобы найти высоту BE выразим площадь треугольника ABD двумя
площадь ABD = AB*BD/2 = AD*BE/2, отсюда
BE=AB*BD/AD=3*4/5=12/5=2,4
Площадь полной поверхности равна
2*площадь основания+площадь боковой поверхности
площадь боковой поверхности = периметр основания умножить на высоту
периметр основания = AB+BC+CD+AD=3+5+3+5=16
тогда площадь боковой поверхности 16*2,4=38,4
площадь полной поверхности
2*12+38,4=24+38,4=62,4
Объяснение:
1) фото чертежа прилагаю...
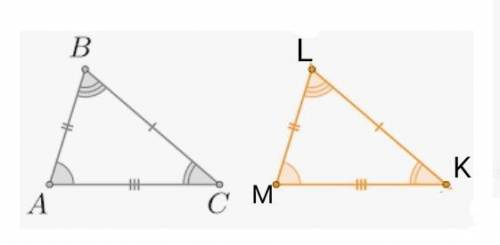
∆ABC=∆MKL
AB=ML
<B=<L
BC=LK
AC=MK
<A=<M
<C=<K
2)
Пусть одна сторона будет х, тогда вторая сторона будет 4х, а третья сторона будет (х-14).
Составляем уравнение
х+4х+х-14=166
6х=166+14
6х=180
х=180/6
х=30 см первая сторона
4*30=120 см вторая сторона
30-14=16 см третья сторона.
ответ: 30см; 120см; 16см
3)
1дм=10см
12дм=120см
1)3+7+5=15 коэффициент
2) 120:15=8 одна часть коэффициента.
3) 8*3=24 см первая сторона треугольника
4) 7*8=56 см вторая сторона треугольника.
5) 5*8=40 см третья сторона треугольника
ответ: 24см; 56см;40см.
Решение задачи с уравнения.
Пусть одна сторона будет 3х см, вторая сторона 7х см; третья 5х см.
Составляем уравнение.
3х+7х+5х=120
15х=120
х=120/15
х=8
8*3=24 см первая сторона
7*8=56 см вторая сторона
5*8=40 см третья сторона.
ответ: 24см; 56см;40см.
окружность является вписанной. стороны угла аод являются половины диагоналей квадрата. следовательно угол фод равен девяносто градусов (так как диагонали квадрата взаимно перпендикулярны и точкой пересечения делятся пополам)