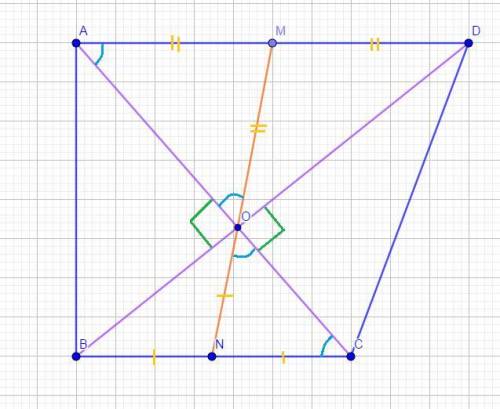
Четырехугольник ABCD, O - точка пересечения диагоналей,
AD || BC и AC ⊥BD,
M - середина AD, N - середина BC,
AD = 12 и BC = 7 (смотрите рисунок).
Найти:Длина отрезка MN.
Решение:Заметим, что O ∈ MN, так как угол MON - развернутый:
∠MON = ∠DOC + (∠DOM + ∠CON) = 90° + (∠OCB + ∠OBC) =
= 90° + 90° = 180°.
Значит, нам достаточно найти длину MO + NO.
Так как треугольник AOD прямоугольный, то медиана MO, проведенная из вершины прямого угла к гипотенузе, равна половине этой гипотенузы (по свойству медианы прямоугольного треугольника):
MO = AD / 2 = 12 / 2 = 6.
Тоже самое можно сказать и о прямоугольном треугольнике BOC с медианой NO:
NO = BC / 2 = 7 / 2 = 3,5.
Значит:
MO + NO = MN = 6 + 3,5 = 9,5.
ответ:MN = 9,5 .
По одному из свойств касательных, проведённых из одной точки, отмеченные лучи являются биссектрисами углов ∠CBА и ∠EDC соответственно; если углы ∠АВС и ∠CDЕ являются равными, то и образованные биссектрисами углы тоже равны (∠ЕDО=∠ОDС=∠СВО=∠ОВА); получаем ΔDОВ с равными углами ∠ОDВ=∠DВО; что значит, что ΔDОВ - равнобедренный; DO=ВО;
Радиус, проведённый в точку касанияПо свойству такого радиуса проведённый отрезок ОС будет перпендикулярен прямой ВD; те OC - высота ΔDOВ; по свойству равнобедренного треугольника OC является и медианой; значит, СD=СВ;
Отрезки касательныхПо свойству касательных, проведённых из одной точки, отрезки ВС, ВА и DC, DЕ касательных попарно равны (те ВС=ВА и DC=DЕ); мы доказали, что DС=ВС; значит, ВС=ВА=DC=DЕ, ч.и.т.д.
№2Обратные теоремы действенны - нужно доказать тоже самое, только в обратную сторону. Поэтому напишу вкратце.
Если АВ=ВС=CD=DЕ, то при ОС⊥ВD ОВ=ОD (св-ва р/б Δ); тогда при ∠ОDВ=∠DВО и биссектрисах DO и ВО (∠ЕDО=∠ОDС и ∠СВО=∠ОВА) ∠ЕDО=∠ОDС=∠СВО=∠ОВА, ч.и.т.д.