Вариант решения.
ответ: 36 ед. объёма
Объяснение:
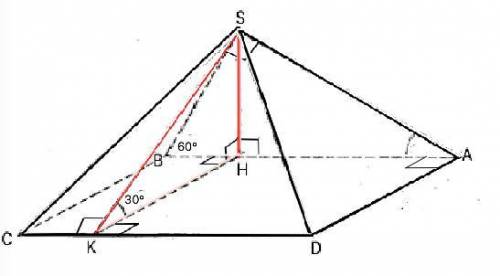
Углы между плоскостями боковых граней и плоскостью основания - двугранные. Их величина определяется градусной мерой линейного угла, сторонами которого являются лучи, проведённые в его гранях перпендикулярно ребру с общим началом на нём. Обозначим пирамиду SABCD . Пусть перпендикулярна плоскости АВСD грань ЅАВ ⇒ её высота ЅН перпендикулярна любой прямой в этой плоскости.
Проведём НК║ВС. Т.к. АВСD прямоугольник, НК⊥СD, и наклонная ЅК⊥CD по т.о 3-х перпендикулярах⇒ ∠ЅКН =30°.
В прямоугольном ⊿ ЅНК с острым углом 30° гипотенуза ЅК=2 катета ЅН, который противолежит углу 30° (свойство) ⇒ 2ЅН+ЅН=9, откуда ЅН=3.
В ⊿ ВЅН угол В=60° ⇒ ВЅ=ЅН:sin60°=2√3
В ⊿ ВЅА гипотенуза АB=ЅВ•cos60°=4√3
В ⊿ ЅКН угол ЅКН=30° ⇒ KH=SH•ctg30°=3√3
Формула объёма пирамиды V=S•h:3, где Ѕ - площадь основания пирамиды, h- её высота. АD=KH=3√3
V=AB•AD•SH/3=4√3•3√3•3/3=36 (ед. объёма).
плоскостью боковой грани угол 30°. Найти:
а) сторону основания
призмы.
б) угол между диагональю призмы и плоскостью основания
в) площадь боковой поверхности призмы.
г) площадь сечения призмы плоскостью, проходящей через диагональ основания параллельно диагонали призмы.
В основаниях правильной призмы - правильные многоугольники, а боковые грани - прямоугольники. Следовательно, ее боковые ребра перпендикулярны основанию.
Треугольник ВD1А - прямоугольный (в основании призмы - квадрат, и ребра перпендикулярны основанию.
а) Сторона основания противолежит углу 30°, поэтому АВ=а*sin 30=a/2
б) угол между диагональю призмы и плоскостью основания - это угол между диагональю ВD1 призмы и диагональю ВD основания.
ВD как диагональ квадрата равна а√2):2
cos D1BD=BD:BD1=( а√2):2):a=(√2):2),
и это косинус 45 градусов.
в) площадь боковой поверхности призмы находят произведением высоты на периметр основания:
S бок=DD1*AB= (а√2):2)*4*a/2=a²√2
г) Сечение призмы, площадь которого надо найти, это треугольник АСК.
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна самой плоскости. Верным является и обратное утверждение.
Высота КН - средняя линия прямоугольного треугольника BDD1. Она параллельна диагонали призмы, а само сечение проходит через диагональ АС основания.
S Δ(АСК)=КН*СА:2
SΔ (АСК)=(0,5а*а√2):2):2=(а²√2):8