проведём диагональ ас, ттогда треугольники асд и авс равнобедренные т к по условию их боковые стороны равны.т.к угол д=39 градусам то угол сад+асд=180-39=141 градус, тогда угол асд=сад=141: 2=70,5 градусам.
рассмотрим треуг. авс:
т.к угол в равен 3 гр,то вас+вса=180-3=177 градусов,по теореме о сумме углов треуг.
т к треуг равнобедренный, то его углы при основании равны,тогда угол вас=вса=177: 2=88,5 градусов
тогда угол а равен сумме углов вас и сад т.е 88.5 градусов+70.5 градусов=159 градусов
ответ: угол а=159 градусов
Окружность с центром О.
ВС - диаметр.
А ∈ окружности с центром О.
∠АОС = 35°
Найти:∠ВАО - ?
Решение:
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
⇒ ∠ВАО + ∠ОВА = 35° (∠АОС = 35°, по условию)
Так как ∠ОВА = ∠ВАО, по свойству ⇒ ∠ОВА = ∠ВАО = 35°/2 = 17,5°
Так как АО и ОВ - радиусы данной окружности с центром О ⇒ △ВОА - равнобедренный.
∠ОВА = ∠ВАО, по свойству равнобедренного треугольника.
Сумма смежных углов равна 180°.
∠АОС смежный с ∠ВОА ⇒ ∠ВОА = 180° - 35° = 145°
Сумма углов треугольника равна 180°.
⇒ ∠ВАО = ∠ОВА = (180° - 145°)/2 = 17,5°
ответ: 17,5°.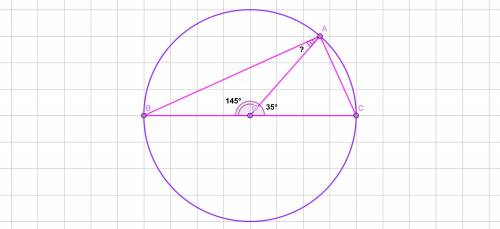
По теореме Пифагора: 8²=4²+R², R²=64-16=48 (см²)
V=Sосн*h/3=пR²h/3=3,14*48*4/3=200,96 (см²)