а) СХ = 1,75 см; XD = 5,25 см;
б) ∠АХС = 116°
Объяснение:
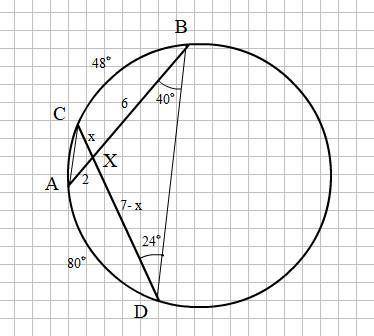
Смотри прикреплённый рисунок.
а)
∠САВ = ∠СDB = 24° так как опираются на одну и ту же дугу ВС = 48°
∠АСD = ∠ABD = 40° так как опираются на одну и ту же дугу AD = 80°
ΔACX ~ ΔDBX по двум равным углам.
Пусть СХ = x, тогда XD = 7 - x
Следовательно, AX : XB = CX : XD
2 : 6 = x : (7 - x)
2( 7 - x) = 6x
14 - 2x = 6x
8x = 14
x = 1.75 (см) - это CX
7 - x = 7 - 1.75 = 5.25 (cм) - это XD
б)
В Δ САХ известны два угла
∠САХ = ∠САВ = 24°; ∠АСХ = ∠АСD = 40°
Согласно свойству углов треугольника
∠АХС = 180 ° - (∠САХ + ∠АСХ) = 180° - (24° + 40°) = 116°
Если нельзя применить теоремы синусов и косинусов, то, скорее всего, можно применить теорему Пифагора.
Пусть высота треугольника АВС из точки А равна Н.
Опустим из основания биссектрисы перпендикуляр h на сторону ВС.
Из подобия треугольников имеем h/H = 4/20 = 1/5,
По Пифагору находим:
Н = √(20² - (5/2)²) = √(400 - (25/4) = √(375/4) = 15√7/2.
Теперь получаем: h = (1/5)*(15√7/2) = 3√7/2.
Длину биссектрисы L тоже определяем по Пифагору.
Проекция её на ВС равна (5/2) + (4/5)*(5/2) = 9/2.
L = √((9/2)² + h²) = √((81/4) + (63/4)) = √(144/4 = √36 = 6.
ответ: длина биссектрисы равна 6.