Угол, косинус которого имеет отрицательный знак, - тупой. Он – смежный острому углу с таким же косинусом со знаком "+".
cos(180°-α)= -cosα
Построим острый угол с положительным косинусом 5/13. Смежным ему будет тупой угол с данным в условии косинусом -5/13.
Косинус - отношение в прямоугольном треугольнике катета , прилежащего к данному углу, к гипотенузе.
Для этого построения нам надо найти второй катет прямоугольного треугольника, в котором один катет равен 5, гипотенуза - 13.
Пусть нам надо построить треугольник АВС с прямым углом С.
Известны гипотенуза АВ=13, катет АС=5
По т. Пифагора ВС²=АВ²-АС²
ВС=√(169-25)=12
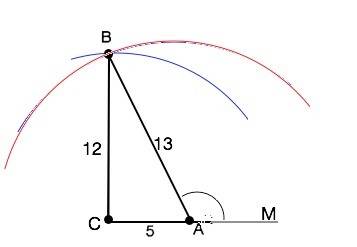
Построение. На луче СМ отложим отрезок АС=5
Из точки А как из центра чертим полуокружность радиусом 13 см.
Из точки С как из центра чертим полуокружность радиусом 12 см.
Точку их пересечения обозначим В.
Соединим А и В. Косинус угла ВАС=АС:АВ=5/13.
Косинус смежного ∠ВАМ= -5/13. Это искомый угол.
Из точки С по общепринятому методу возводим перпендикуляр. На нем откладываем катет СВ=12 см.
Соединяем В и А. В построенном треугольнике косинус угла А равен 5/13. Смежный ему тупой угол ВАМ - искомый, его косинус - 5/13.
Проведем из тупого угла меньшего верхнего основания высоту, получим прямоугольный треугольник, со гипотенузой, она же и большая бок. сторона, и острым углом в 45°, значит, катеты в этом треугольнике рвны по 12, т.к. гипотенуза 12√2.
Воспользуемся свойством трапеции, в которую можно вписать окружность, тогда сумма оснований = сумме бок. сторон, но одна сторона у нас 12см, меньшее бок. сторона, она же и высота, а другая большая, равна 12√2
Площадь равна 12√2*(12+12√2)/2=12√2*(6+6√2)=(72√2+144)/см²/