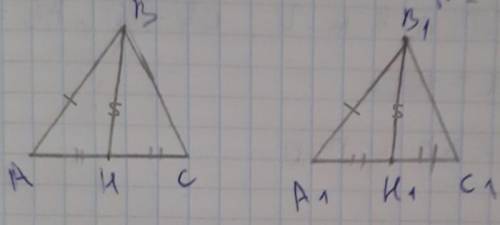
Итак, было дано, что треугольники АВС = А1В1С1. Из этого следует, что медианы ВН = В1Н1 (медианы в равных треугольниках, проведённые к равным сторонам, равны). Также, АВ = А1В1.
Рассмотрим треугольники АВН и А1В1Н1. АН = НС, но также А1Н1 = Н1С1, а учитывая равенства треугольников АВС и А1В1С1, получаем. что отрезки АН = А1Н1. Следовательно, треугольники АВН и А1В1Н1 равны по трём сторонам.
ответ:
объяснение:
1. рассмотрим параллелограмм авсд.
s=ah, а= 6 это следует h=4
2.рассмотрим δ аве, в=5, h=4. тогда по теореме пифагора
хво2степени =5 в степени2 - 4 в степени2 =9
х=3, т.е. ае=дк=3, это следует
3. ед=ад-ае=3
4. рассмотрим δвед, по теореме пифагора следует
хво 2 степени=3во 2степени+4во второй степени=25
×=5,т.е. вд=5
5.проведем дополнительную высоту ск с вершины с и соединяем с основанием ад
6. рассмотрим δ аск, ак=9, ск=4⇒ по теореме пифагора
хво 2степени=9во2степени+4 во 2степени=97
×=√97, т.е. ас=√97
точка а находится на одинаковом расстоянии от всех вершин равностороннего треугольника, => точка а проектируется в центр правильного треугольника.
найти длину перпендикуляра н.
центр правильного треугольника - точка пересечения медиан, высот, биссектрис, в которой они делятся в отношении 2: 3, считая от вершины.
высота h правильного треугольника вычисляется по формуле: h=a√3/2.
h=(4√3)*√3/2, h=6 см.
рассмотрим прямоугольный треугольник: катет - высота н, катет - (2/3)h=4 см, гипотенуза - расстояние от точки а до вершин треугольника =5 см.
по теореме пифагора: 5²=н²+4². н=3 см
ответ: расстояние от точки а до плоскости треугольника 3 см
∆АВС = ∆А1В1С1, => все стороны и углы этих треугольников между собой равны.
Рассмотрим ∆АВН и ∆А1В1Н1:
∠А = ∠А1, так как треугольники АВС и А1В1С1 равны.
АВ = А1В1, так как треугольники АВС и А1В1С1 равны.
Так как ВН и В1Н1 - медианы => они делят стороны АС и А1С1 на 2 равные части.
=> АН = А1Н1.
=> ∆АВН = ∆А1В1Н1, по 1 признаку равенства треугольников.
Ч.Т.Д.