81√3 ед²
Объяснение:
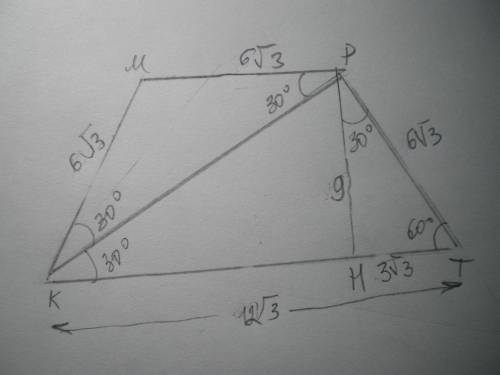
Дано: КМРТ - трапеция, КМ=РТ, ∠Т=60°, КР⊥РТ; КТ=12√3. Найти S(КМРТ).
Рассмотрим ΔКРТ - прямоугольный; ∠РКТ=90-60=30°, значит, РТ=0,5КТ=6√3 по свойству катета, лежащего против угла 30 градусов.
Проведем высоту РН и рассмотрим ΔРТН - прямоугольный;
∠ТРН=90-60=30°, значит, ТН=0,5РТ=3√3.
Найдем РН по теореме Пифагора:
РН²=РТ²-ТН²=108-27=81; РН=9.
Найдем МР. ∠МРК=∠РКН=30° как внутренние накрест лежащие при МР║КТ и секущей КР; ∠МКР=60-30=30°, значит, ΔКМР - равнобедренный, МР=КМ=6√3.
S(КМРТ)=(МР+КТ)/2 * РН = (6√3+12√3)/2 * 9=(9√3)*9=81√3 ед²
По условию KL = KC + LC
Отрезки касательных проведенные из одной и той же точки к одной и той же окружности равны.
Тогда
KC = KA
LC = LB
Следовательно KL = KC + LC = KA + LB
Подставим это в первое равенство
Периметр треугольника KLM = MK + ML + KL =
= MK + ML + KA + LB =
= MK + KA + ML + LB
Очевидно что
MK + KA = MA
ML + LB = MB
Тогда
Периметр треугольника KLM = MK + ML + KL = MA + MB
Последнее выражение (MA + MB ) не зависит от С
Следовательно периметр треугольника KLM не зависит от выбора точки С
что и требовалось доказать.