Объяснение:
По определению, две прямые параллельны, если существует плоскость в которой лежат две эти прямые, и они там параллельны. Отметим на данной прямой точки A и B. А точку обозначим как O. Пусть через точку О проходят две прямые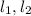 
параллельные AB. Пусть 
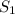-- плоскость, содержащая одновременно 
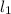и AB (эта плоскость существует из определения). Аналогично определяем плоскость 
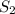. Заметим, что 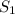и 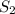проходят через точки O, A, B. Но по аксиоме через три точки, не лежащие на одной прямой проходит только одна плоскость. Значит плоскости 
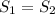= S совпадают. (назовём их общим именем S). Рассмотрим плоскость S: в ней лежат точки O, A, B и две прямые 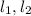. Причем, 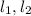проходят через точку O и параллельны AB. Но по аксиоме планиметрии (напомню, мы сейчас живем в плоскости S для которой выполнены все аксиомы планиметрии) через точку O может проходить лишь одна прямая, параллельная AB. Значит 
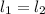, ч.т.д.
р = (6+7+5)/2 = 9
S = √(9(9-6)(9-7)(9-5)) = √216 = 14.69693846
r = S / p = 14.69693846 / 9 = 1.63299316.
Так как треугольники подобны, то площади пропорциональны квадрату коэффициента пропорциональности.
Найдем высоту треугольника АВС:
Hb= 2S / b = 2*14.69693846 / 7 = 4.1991253.
Высота треугольника ВКМ меньше на 2 радиуса:
hb = Hb - 2r = 4.1991253 - 2*1.63299316 = 0.93313895
Коэффициент пропорциональности к = hb / Hb = 0.9331389 / 4.1991253 = 0.22222222,
к² = 0.04938272.
Тогда S(BKM) = 14.69693846* 0.04938272 = 0.725774739 кв.ед.
А периметр равен Р(АВС)*к = (6+7+5)*0.22222222 =
= 18*0.22222222 = 4.
2) В этой задаче не улавливается зависимость между заданными площадями треугольников.
3) В этой задаче что то неверно в условии.
Если диаметр , проходящий через вершину В, делит хорду KL пополам, то эта хорда перпендикулярна диаметру. При этом она не пересекает сторону ВС - смотри прилагаемый чертёж.