S1 ≈ 19,8 cм².
S2 ≈ 3,9 cм².
Объяснение:
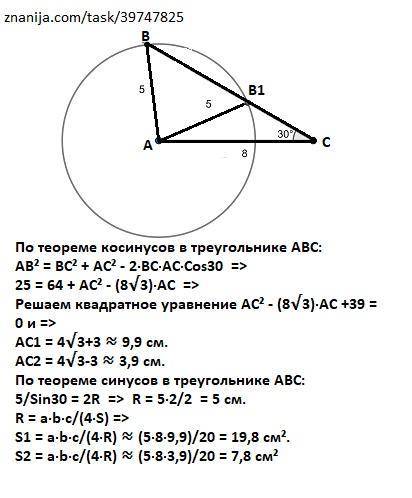
По теореме косинусов в треугольнике АВС:
АВ² = ВС² + АС² - 2·ВС·АС·Сos30 =>
25 = 64 + AC² - (8√3)·AC =>
Решаем квадратное уравнение AC² - (8√3)·AC +39 = 0 и =>
AC1 = 4√3+3 ≈ 9,9 см.
АС2 = 4√3-3 ≈ 3,9 см.
По теореме синусов в треугольнике АВС:
5/Sin30 = 2R => R = 5·2/2 = 5 см.
R = a·b·c/(4·S) =>
S1 = a·b·c/(4·R) ≈ (5·8·9,9)/20 = 19,8 cм².
S2 = a·b·c/(4·R) ≈ (5·8·3,9)/20 = 7,8 cм²
P.S. Для проверки на рисунке выполнено точное построение, доказывающее, что задача имеет два решения.
1) B=D=126°(как внутренне накрест лежащие):Сумма всех углов параллелограмма равна 360°,следовательно угол A+C=360°-(126°+126°)=108°, угол А=108°/2=54°,угол А=углу С=54°
2)P=36см,к пример сторону 1 и 3 примем за 1х+1х,стороны 2 и 4 за 2х+2х,сумма всех сторон равна : 6х=36,из этого х=6,дальше :сторона 1 равна 1х=6,сторона 2 равна 2х=12,сторона 3=стороне 1,а сторона 4= стороне 2
3)P=40дм=400см,у параллелограмма сторона 1=стороне 3,а сторона 2=стороне 4,следовательно: сторона 1=3х,2=2х,сторона 1=3,сторона 2=4
сумма всех сторон равна 400см=10х,х=40.Сторона 1 равна 120см,сторона 3 =стороне 1=120см,сторона 2 равна 80см,сторона 4=стороне 2=80см
4)Сумма углов параллелограмма=360°,из этого следует что угол D=360°-237°=123°,угол В=углу D=123° (как накрест лежащие),угол А+С=237°-123°=114°,угол А=114°/2=57°,угол С=углу А=57°