cos∠B = 0
cos∠A = 0,6
cos∠C = 0,8
Объяснение:
Найдем длины сторон треугольника по формуле расстояния между точками:
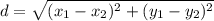
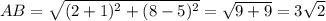
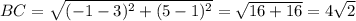

Проверим по теореме, обратной теореме Пифагора, не является ли этот треугольник прямоугольным:
AC² = AB² + BC²
(5√2)² = (3√2)² + (4√2)²
50 = 18 + 32
50 = 50 - равенство верно, значит треугольник прямоугольный с гипотенузой АС.
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе.
Косинус прямого угла равен нулю.
cos∠B = 0
cos∠A = AB / AC = 3√2 / 5√2 = 3/5 = 0,6
cos∠C = BC / AC = 4√2 / 5√2 = 4/5 = 0,8
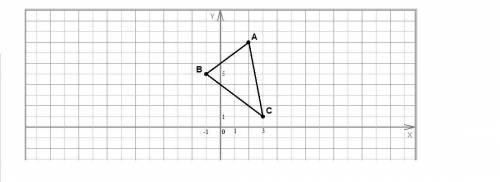
Объяснение:
радиус основания конуса
R=4√3 см
угол между образующей и плоскостью основания
α=30°
найти
высоту Н,
образующую L ,
площадь осевого сечения конуса
S - ?
1)
образующая
L=R÷cosα=4√3 ÷cos30°= 4√3 ÷√3/2=4√3×2/√3=4×2=8см
высота конуса по теореме Пифагора
H=√L²-R²=√(8²-(4√3)²)=√64-48)=√16=4 см
2)
осевое сечение правильного конуса имеет вид равнобедренного треугольника, где диаметр D=2R=b конуса основание b равнобедренного треугольника, а образующая L =a две равные боковые стороны. высота конуса Н является высотой треугольника .
D=b=2×4√3=8√3 см
S=1/2 ×b×H=1/2 × 8√3 ×4=16√3 см²