АВСД - рівнобічна трапеція, де АВ=СД=10см (бо бічні сторони у рівнобічної трапеції рівні), а ВС та АД - це основи трапеції. В трапецію можна вписати коло, якщо сума довжин основ рівна сумі довжин бокових сторін, тобто
АВ+СД= ВС +АД
10+10=ВС+АД
ВС+АД=20
Формула визначення радіуса вписаного в трапецію кола: r = h/2, де r - це радіус кола, а h - це висота трапеції h=2* r=2*4=8см Формула площі через основи та висоту: S = (ВС + АД)· h/2 Раніше ми знайшли, що ВС+АД=20см, що і підставимо у формулу: S = 20· 8/2 S =80 см²
Відповідь: площа трапеції, яка описана навколо кола = 80 см²
а) ∠В = 30°, АВ=4 см, AD=ВD=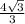 см ∠D=120°
см ∠D=120°
б) S = 2√3 cм²
Объяснение:
а) Сумма острых углов прямоугольного треугольника равна 90°
∠В=90°-∠А=90°-60°=30°
Катет прямоугольного треугольника, лежащий напротив угла в 30° равен половине гипотенузы.
⇒ АВ=2*АС=2*2=4см
По теореме Пифагора найдём катет ВС:
ВС = 2√3 см
Биссектриса угла треугольника делит противолежащую сторону в отношении длин прилежащих сторон.Рассмотрим ΔABD: ∠ВАD=30° - так как AD – биссектриса, ∠В=30° ⇒ ΔABD- равнобедренный, AD=ВD=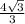 см
см
Так как сумма углов треугольника = 180°, то
∠АDB = 180-∠ВАD-∠В=180-30-30=120°
б) Площадь прямоугольного треугольника равна произведению двух его катетов деленное на 2:
S = 2√3 cм²