Объяснение:
Дано:равностор.Δ
h = 6√3
Найти: а
Т.к. треугольник равносторонний, то его стороны равны. Пусть сторона а, тогда высота делит сторону на два части, по а/2, и образует два равных прямоугольных треугольника, в которых а - гипотенузы, и а/2 - катеты.
По теореме Пифагора:
а² = (а/2)² + (6√3)² ; а² = а²/4 + 36*3;
3а²/4 = 36*3 ; а² = 36*4; а =12
ответ: а = 12
S∆JAB=12см²
Sпр=120см²
Объяснение:
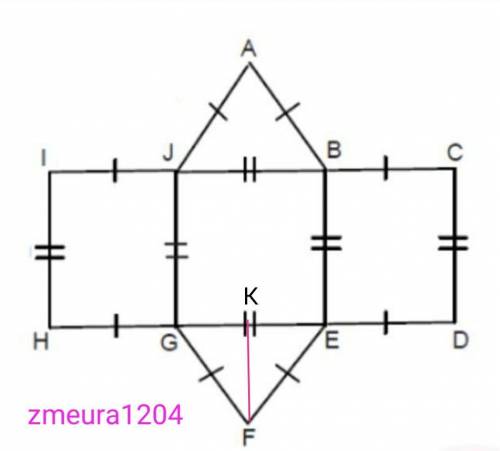
Данная фигура треугольная призма в основании равнобедренный треугольник.
GF=FE=5см, по условию.
ЕВ=ВJ=JG=GE=6см по условию это квадрат.
Проведём в треугольнике ∆GFE, высоту FK.
FK-высота и медиана, так как треугольник равнобедренный.
КЕ=GE:2=6:2=3см.
∆КFE- прямоугольный треугольник.
По теореме Пифагора
КF=√(FE²-KE²)=√(5²-3²)=√(25-9)=4 см
S∆FGE=1/2*KF*GE=1/2*4*6=12 см².
S(GJBE)=BE²=6²=36см²
S(BCDE)=BC*CD=5*6=30 см²
S∆FGE=S∆JAB.
S(BCDE)=S(IJGH)
Sпр=2*S∆FGE+2*S(BCDE)+S(GJBE)=
=2*12+36+2*30=24+36+60=120см² площадь полной поверхности призмы.
Назовем наш треугольник ABC, проведем высоту BL, длина которой равна 6√3. Известно, что высота в равностороннем треугольнике делит сторону на две равные части, при этом возникают два одинаковых прямоугольных треугольника, тогда рассмотрим один из них, ALB. Обозначив АL как х, АВ как 2х, можем найти их длины, применив теорему Пифагора:
(2x)^2 = x^2 + (6√3)^2,
3x^2 = 108,
x = 6, тогда AB = 12, тогда периметр равностороннего треугольника:
Р = 3 * AB = 3 * 12 = 36 .
ответ: 36
Объяснение: