ответ: 1. Знайдемо координати точки М, яка є серединою сторони АС за формулою ділення відрізка на дві рівні частини:
Хм=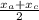 
= 
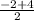=1; Yм=
=
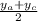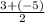= -1
Отже, координати точки М (1;-1).
2. Довжину медиани знайдемо, як відстань між двома точками за формулою:
BM =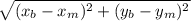 
=
= 
одиниць.
3. Рівняння медиани ВМ запишемо, скориставшисьформулою рівняння прямої, щопроходить через дві точки:
= 
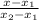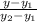
Підставивши координати точок В(0;1) і М(1;-1) запишемо загальне рівняння медиани ВМ:
;
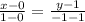х=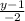
;
-2х=у-1;
-2х-у+1=0.
Для знаходження рівняння з кутовим коефіцієнтом kВМ медиани ВМ, розв"яжемоотримане рівняння відносно у:
у= -2х+1, звідси k=-2.
Відповідь: довжина медиани одиниць, загальне рівняння медиани -2х-у+1=0, рівняння з кутовим коефіцієнтом у=-2х+1.
Малюнок до задачі в додатку.
Объяснение:
Слегка такое "нестандартное" решение. Но - только слегка.
Если из одной из точек касания провести диаметр и его конец соединить с другой точкой касания, то получится прямоугольный треугольник (третья сторона - сама хорда, конечно), с гипотенузой 20 и катетом 16, то есть "египетский" треугольник (12,16,20). При этом угол между сторонами 12 и 20 измеряется половиной дуги, стягиваемой хордой.
С другой стороны, если рассмотреть прямоугольный треугольник, образованный хордой (её половинкой), касательной и частью линии, соединяющей точку С с центром, то угол при точке касания тоже измеряется половиной этой дуги. Поэтому это треугольник подобен треугольнику (12, 16, 20), при этом меньший катет равен 16/2 = 8, откуда АС = 20*8/12 = 40/3.